Risk assessment of migration from packaging materials into food
Yan Zhua, Phuong-Mai Nguyenb, Olivier Vitraca†
aINRA, French National Institute of Agricultural Research, UMR 1145 Ingénierie Procédés Aliments, AgroParisTech, INRA, Université Paris-Saclay, 91300, Massy, France
bLNE, French National Laboratory of Metrology and Testing, 29 Avenue Roger Hennequin, 78197 Trappes Cedex, France
Abstract
This chapter reviews the principles to assess the risk of migration from food packaging materials and related application of such materials. The point of view considered in this chapter is that most of the past crises involving materials could have been avoided with a correct appraisal of mass transfer and the use of numerical tools. Migration modeling is broadly available today and accepted in major global regulations. This chapter does not advertise any platform but shows how their basic or advanced use can prevent the risk of migration regardless of existing or preexisting regulations. Risk assessment is proposed as a generic tool to revise the formulation of materials (thermoplastics, varnishes, coatings, lacquers, inks…), to optimize packaging design and supply chains, to promote new molecular design of additives, to devise improved recycling procedures, to accelerate the acceptation of new polymers and materials (e.g., biosourced, biodegradable, recycled, with repeated use).
Risk assessment of migration from packaging materials into foodAbstract2 Introduction3 What did we learn from crises?3.1 A short history3.2 Why thermodynamics counts3.3 Modern crises4 Risk assessment for decision making4.1 Overview of migration modeling4.1.1 What is currently permitted?4.1.2 Modeling using a tiered approach: from worst-case scenarios to detailed conservative ones4.1.3 Key steps in migration modeling and risk assessment approaches4.2 Migration modeling for compliance testing and beyond4.2.1 Principles of migration modeling4.2.1.2 Migration modeling and similitude properties4.2.1.3 Explicit vs implicit food representation4.2.1.4 Other assumptions4.2.2 Governing equations for monolayer materials4.2.2.1 Overview4.2.2.2 Concentration in the contact phase at thermodynamical equilibrium4.2.2.3 Dimensionless migration kinetics and their analytical approximations4.2.3 Governing equations for multilayers4.2.3.2 Concentration in the contact phase at thermodynamical equilibrium4.2.3.3 Transport equations4.2.3.4 Limiting mass transfer resistance4.2.3.5 Typologies of migration behaviors4.2.3.6 Superposition principles and conservative scenarios for multilayer and multicomponent systems4.2.4 Strategies and equations to simulate multiple steps and conditions 4.2.4.1 Problem formulation4.2.4.2 A first intuitive approach4.2.4.3 Strict conditions of exchangeability with explicit food models 4.2.4.4 Conditions of exchangeability in food implicit models4.2.5 Discussion on the choice of accelerated conditions and the identification of critical steps4.2.5.1 Factors of acceleration and possible biases. 4.2.5.2 Causality, critical steps, and crtical components. 5 Diffusion properties in polymers5.1 Definitions of diffusion coefficients5.1.1 Self- and trace-diffusion coefficients5.1.2 Mutual diffusion coefficients5.2 Effect of the geometry of migrants on $D_p$ values5.3 Effect of the polymer;5.4 Activation of diffusion by temperature6 Sorption properties and partition coefficients6.1 Some definitions6.1.1 Chemical potentials, fugacities, and activities6.1.2 Effective partition coefficients between P and F6.2 Sorption isotherms6.2.1 Linear isotherms6.2.2 Binary Flory isotherms6.2.3 Ternary Flory isotherms6.2.4 Binary Flory-Huggins coefficients in a copolymer AB6.3 High throughput calculations of Flory-Huggins coefficients at atomistic scale6.3.1 Justification and limitations6.3.2 Principles7 Probabilistic modeling of the migration7.1 Beyond intuition7.2 Epistemic uncertainty7.3 Sensitivity analysis of migration models7.3.1 Local sensitivity analysis7.3.2 Global sensitivity analysis via stochastic simulation7.4 Principles of the probabilistic interpretation of mass transfer7.4.1 Input distributions7.4.2 Estimation of probabilities via Monte-Carlo sampling7.4.3 Estimation of joint probabilities via the composition theorem7.4.2 Some illustrations7.4.2.1 Typical probabilistic migration kinetics7.4.2.2 Effect of Bi and sD8 What will be the future?8.1 Extending the legal scope of migration modeling8.2 Extending the capacity of migration modeling8.3 Bridging migration modeling, safe-by-design, and ecodesign approaches8.4 Online resources ease risk assessment8.4.1 Lower bounds of toxicological thresholds for non-evaluated substances8.4.2 Migration modeling tools9 References
2 Introduction
What is migration?
Migration is a general term for spontaneous mass transfer of chemical substances, and, in the context of food packaging, it indicates an extraction of packaging constituents and their transfer to the food. Industry and authorities recognized the fate of cross mass transfer between materials and the resulting contamination of the food evenly. The term migration was consequently preferred to the contamination one in the scientific literature and legal documents. During the last decades, the concern about the safety of food contact materials (FCM) raised with our appetite for transformed food and ready to eat meals, and with our always growing needs for disposable packaging. Nowadays, FCM is identified as the prevalent source of exogenous chemical contaminants in food, ahead of pesticides, veterinary drug residues and other environmental contaminants . The ubiquitous contamination issue was thought to be restrained initially to contact layers and materials, but it is far from being the case. Modern food packaging systems are, indeed, printed, coated, laminated and associated with other materials. The whole history of these materials must be considered, as they may have been subjected to repeated use, brought to a second life via a recycling process, stored in reels or stacks contacting internal and external surfaces; shipped with other materials during long and warm periods. The whole contamination problem can be envisioned as a cross mass transfer of several substances between Matryoshka or nesting dolls. The pre-weighted food feeds the smallest doll and is surrounded by many layers including the rigid walls of the primary packaging, a sleeve, the transport cardboard box containing several sale units, the treated wood pallet, a wrap cling film, etc. until the freight container. In ready to eat meals and convenience foods, additional components may be present internally such as a bag preventing direct contact with walls, individual packages or wraps for portion control, separators and specific holders, sachets for seasonings, active elements to increase food shelf-life, etc. The whole picture is not complete without citing the many tie layers, the glued labels, the printed and coated surfaces. The ultravacuum and aerospace industry would have regarded similar materials and combinations as a substantial reservoir of organic compounds without exception. As an illustration, the NASA compiled more than 35,000 outgassing data 1, for almost any material, which could enter in a spacecraft, including many commodity materials such as thermoplastics, coatings, and tapes.
Our approach to risk assessment
This chapter provides a comprehensive description of molecular processes responsible for the migration of packaging constituents and their pathways to the food with or without direct contact. The recurring structure of contamination scenarios leading to the past major crises is discussed and analyzed regardless of the modalities of their regulations. The distance between the facts and practices is maintained all along this chapter, as the regulations and the good manufacturing practices follow the crises and rarely precede them. Major regulations (the US, European and Chinese) are sketched to highlight their convergence on the use of modeling to demonstrate compliance and to evaluate the safety of recycled materials. The miscalculation of the connection between chemical structure and physicochemical properties (volatility, solubility, diffusivity) has been the foremost cause of past crises. Computer and proper simulation procedures can assist efficiently small and intermediate industries in overcoming internal knowledge limitations on materials, mass transfer, and physical-chemistry. By comparing with acceptable thresholds, migration modeling can be extended at low cost to non-evaluated and non-intentionally added substances. In the foreseeable future, similar techniques might be used to tackle the diffuse risks raised by endocrine-disrupting chemicals 3, 4 alone or in mixing cocktails 5. More globally, the extension of predictive tools and approaches will benefit not only the evaluation of the contribution of food contact materials to the global exposome 6, but it will also facilitate the adoption of preventive approaches all along the supply chain. Safe-by-design approaches, including additive redesign, optimization of the formulations (choice of substances and amounts), new packaging design and good manufacturing practices, will reduce the risk of unintended food packaging-interactions 7, 8. Improving the way food ingredients are stored and processed will bring additional risk reduction, beyond the reduction of the migration in the finished product.
The scope of migration modeling
The scope of migration modeling has been underestimated in the past and limited to compliance testing under worst-case scenarios. The uncertainty and the pioneered methods were too coarse thirty years ago. We suggest that the scope can be broadly extended today as shown in Figure 1. Earlier models could cover only single materials, simple geometries without any dynamic change of conditions. The most advanced models can today incorporate information at molecular scale and cover an entire supply chain. The chapter focuses on the key details and features required to get robust modeling of migration at the scale of a material, component (label, cap…), of an entire food packaging, of industrial practices. The methodology to get estimates of consumer exposure are not covered in this chapter because they are directly related to the design of the packaging itself.
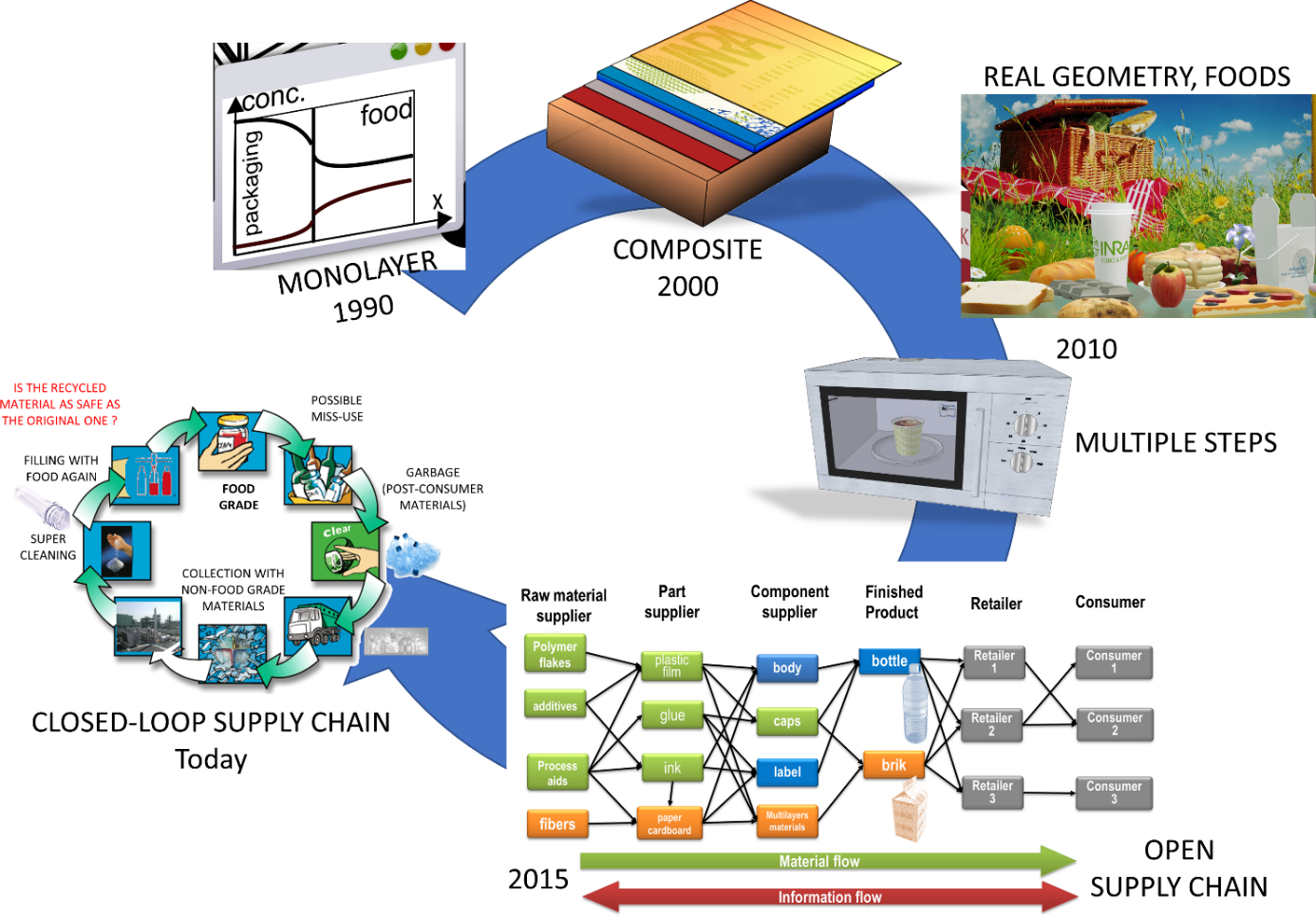
Figure 1. Evolution of the scope of migration modeling during the last decades
Beyond migration modeling: a holistic science
Once used, the packaging losses all its value, but its cost remains high for the environment. Revised versions of life-cycle-analysis propose to add chronic effects on health due to long-term impacts on the environment9-11. We promote this initiative for applications in food contact but also for cosmetics, pharmaceutical, medical, biotechnological ones and for any situation where the release of chemicals by materials is of concern (e.g., occupational exposure). Innovations could come shortly at the cost of a full revisitation of our engineering practices. A global science needs to emerge beyond common mistaken beliefs: migration can be avoided, biosourced materials are safer, biodegradable as recycled materials can be used without a safety assessment. We do not pretend to cope with all problems, but we suggest thoughtful routes to evaluate the risks of contamination at any stage of the supply chain and consequently to measure the benefits of alternative solutions. From step to step, we could approach better inertia as it has been achieved to minimize outgassing in ultravacuum systems.
3 What did we learn from crises?
Highlights on crises associated with food contact materials
- The contamination of food by materials in contact is never fortuitous, but it may be not avoidable.
- Only the nature of the migrating substances, the extent of the migration can be controlled by our choices.
- Most of all crises if not all could have been predicted with relatively simple descriptions of mass transfer phenomena and thermodynamics.
- As a corollary, consumer exposure to substances from food contact materials could be reduced.
3.1 A short history
Crises tend to predate regulations and frequently them — we coin crisis a situation where food safety is seriously questioned due to systematic contamination by one or several FCM. The contamination was usually unexpected but not unforeseeable due to its anthropogenic nature. Comparatively to food infection and food intoxication, the possibility of crises by FCM substances has been recognized lately in Europe. The obligation of traceability of all packaging components to organize the recall of packaged food products were implemented only in 2004 through the framework regulation 2035/2004/EC.
Thirty years ago, western governments endorsed enthusiastically an early idea hypothesized by Jerome Nriagu 12 and popularized by Clair Patterson 13, whereby Roman civilization collapsed as a result of lead poisoning. “Although today lead is no longer seen as the prime culprit of Rome’s demise” (quoting 14), lead poisoning from leaded pottery and earthenware was known for centuries. All possible sources of lead were individually tracked by authorities in the nineteenth century, in particular, after the development of wrought-iron canisters. The French ordinance of March 21th, 1879 (see p 231 of 15) prohibited, for instance, the use alloys of tin and lead for all inner parts including welding. The French regulation of 1908 was even more explicit “no food substance should contain any harmful product or chemical substance” 16. In modern times, the editorial of the New England Journal of Medicine was heading in 1972 “The invisible pollution” 17 after the discovery of plasticizers in human blood stored in polyvinyl chloride (PVC) bags 18, 19. Similar contaminations were associated with tubbing used for culture tissues 20. The exact nature of the contamination mechanism was not fully established at the time, and an analogy with the corrosion of metallic materials was falsely suggested 21. The first mechanistic review of what called “extractivity” or “migration propensity” appeared only in 1980 22, 23. Three mechanisms of contamination were listed:
- contamination only from the extreme surface of the material in contact;
- the diffusion-controlled release of the material in contact;
- penetration of the polymer matrix by the contacting phase (liquid) and subsequent extraction of materials constituents.
Early descriptions were strongly influenced by the behavior and the dominance of PVC in the seventies and eighties, and by the lack of sensitivity of contemporaneous analytical techniques. In spite of erratic results and difficulties in getting reproducible kinetics, the corollary reasoning supported the confidence of stakeholders in the apparent inertia of thermoplastics and thermosets lastingly. It was falsely thought that:
- the absence of direct or permanent contact,
- aqueous contact,
- high molecular weight additive or residues,
- low temperatures
would prevent any significant migration and do not need proper attention. At the time, only a study using radio-labeled additives 24-27 carried out under contract for the Food and Drug Administration and, subsequently, interpreted in detail during the Ph.D. thesis of Thomas P. Gandek at MIT 28 highlighted several abnormalities, which were anticipating future crises. In poor barrier polymers, the hydrodynamic conditions in the contacting liquid were showed to control the release; but neglecting it them was not underestimating migration, on the contrary. In aqueous food simulants and presumably in any aqueous-type food, the decomposition of additives displaces continuous the apparent thermodynamical equilibrium between the material and the liquid in contact. Contrary to previous descriptions, the contamination was found unbounded 29, 30.
Similar conclusions were found for large additives migrating to dry food simulants for short periods at temperatures elevated but sufficiently close to those met during transportation 27. The most outstanding finding was that the migration rate could not be overestimated by experiments using corn oil. Accelerating testing using food-simulating liquids is a common practice to evaluate the risk of migration, but it was emphasized that more rationale was required for evaluating with sufficient confidence the risk of migration for new polymers. Simulating liquids should be chosen respectively to the nature of both the migrating substance and of the original polymer. Fatty food simulants offer worst-case migration and extraction capabilities only for hydrophobic substances in apolar polymers. Aqueous simulants are more aggressive for polar or charged substances, and polar polymers 31. Since most of the food products are multicomponent and multiphasic (e.g., emulsions, gels, cake with chocolate, etc.), they cannot be reduced easily to a single contact phase when different classes of migrants are involved.
3.2 Why thermodynamics counts
Thermodynamics has been praised by the whole packaging community, including the chemical, compounding, processing, recycling and food industries, as well as authorities and safety agencies. It has been regularly as the primary argument to justify the conditions of compliance testing (choice of simulant, test temperature and contact time, extrapolation rules and migration calculations) and to authorize recycling process of polymers, active packaging, etc. A naïve reasoning may, however, lead to severe consequences, which should be underestimated. A common mistake is to assume that mass transfer stops after some long time. The transferred amount is assumed to reach, indeed, a maximum controlled by the partition coefficient between the packaging and the food. Statistic mechanics teaches us that this macroscopic description is oversimplified and proceeds with an analogy between a mechanical equilibrium and a chemical equilibrium. At molecular scale, all the substances continue to move freely at equilibrium as they were moving before the whole packaging-food system reaches a macroscopic equilibrium. In a closed system, the equilibrium is associated to a zero net mass balance across the packaging-food interface: the number of molecules of type A entering in the food is exactly compensated by the number of molecules of type A leaving the food. We might think that because the food has a larger volume than the packaging, the return of molecules is unlikely. It is however not correct because the substances are transported faster in food than in dense polymer matrices. Only when the volume ratio food-to-packaging becomes very large, the probability of return approaches zero and a total extraction of A is expected regardless of its affinity for the food.
When a chemical reaction transforms the species A into the species B in the food, the previous balance is profoundly modified, and more substances A are invading the food than substances A returning to the packaging. Similarly, when the substance A cleaves into two breakdown products and in the packaging, parts of substances A that migrated in the food are partly reabsorbed by the packaging itself. When the reaction is almost complete, only traces can be identified in the food. On the opposite, substances and can migrate (faster than A) and may remain undetected if not specifically targeted.
Adding more packaging components (several layers, cap, label, etc.), variable temperatures and complex contact conditions complicate the mass transfer description, but thermodynamics always provides the relationships to encompass all possibilities of exchanges including in multiphasic foods. The thermodynamics needed is not equilibrium thermodynamics, as it ignores the time-course of the migration processes, but a local version, where equilibrium is reached only at the interface between each phase and component. The classical non-equilibrium thermodynamical concept of local thermodynamic equilibrium is robust enough to integrate non-linear sorption isotherms, coupled mass transfer and plasticizing effects. When the relaxation of polymer systems is longer than the timescale of mass transfer (e.g. , in glassy materials, hysteresis effects), constitutive equations need to be modified to integrate the mechanical behavior of the materials (swelling or densification).
No food packaging system is enough isolated from the rest of the world so that a true thermodynamical equilibrium cannot be finally observed literally in real-life systems. Preventing the loss with surroundings in tests and calculations maximizes the amount transferred to the food. Conversely, not considering the possibility of redistribution of migrants between materials during their lifetimes hampers the proper management of non-intentionally added substances.
In shorts, most of the experimental evidence supporting regulation and rules were obtained on simple materials, preferably monolayer and apolar ones at rubber state. Equilibrium was reached rapidly in conditions accelerated comparatively to the real shelf-life of food products. In this case and only in this case, the concentration in the simulating liquid increases monotonously with time.
Thermodynamics offer a robust framework to address all previous issues at the scales of molecules, where the interactions and the macroscopic properties emerge from the vibration of atoms. Theories or robust inference rules have been developed to relate the chemical structure of the migrants and the polymers to the diffusion and partition coefficients, without requiring an explicit description of molecular interactions. The principles of quantitative structure-relationships detailed in this chapter are sketched in Figure 2. They should not be considered as definitive rules, but as an ongoing process, where updates are regularly obtained.
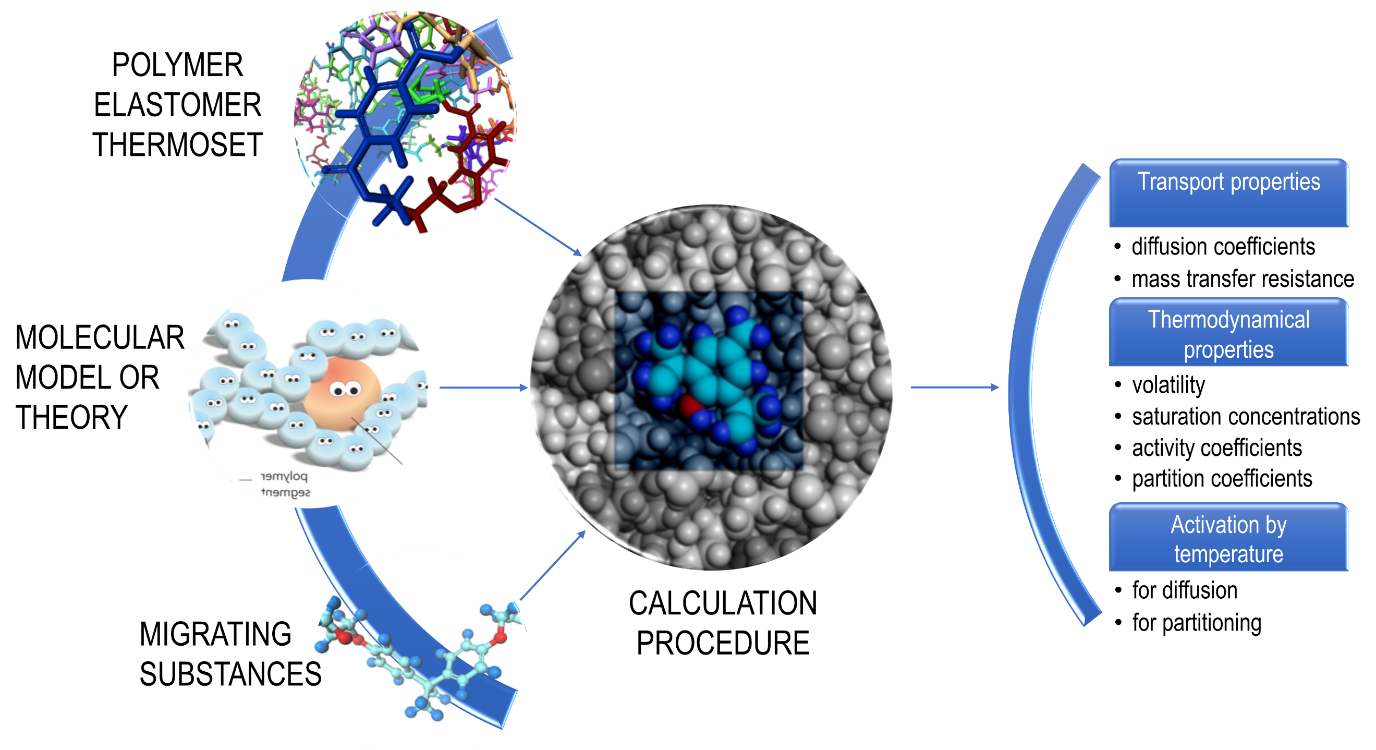
Figure 2. Principles of quantitative structure relationships to predict common transport and thermodynamic properties needed for migration modeling.
3.3 Modern crises
“Early civilizations adopted laws that punished sellers of tainted food” as quoted by Merill 32, In 1958, the US Food, Drug and Cosmetic Act introduced the Delauney clause, which prohibits the use of any substance as food additive “if it is found to induce a cancer when ingestion by man or animal” 33. In the US regulation system, the concept of additives is broad and comprises substances, which may become a component of food or otherwise may affect the food characteristics 34. They include therefore any substance released by food packaging, regardless of the nature of the materials. As a result, it is the responsibility of the industry to submit a dossier to the Food and Drug Administration (FDA) to get a new substance, a new polymer and new application of packaging approved. Similar rules were enforced successively in EU via the directive 1990/128/EEC 35, the regulations 2002/72/EC 36 and 10/2011/EC 37. The dossiers apply, however, only to initial substances of plastic materials monomers and additives. China adopted recently legal requirements close to the European system for plastics with a premarket approval for both the plastic resins and the additives 38. The inventories of substances are compared in Table 1.
Table 1. Comparison of the Inventories of food contact substances in US, EU and China. Sources 37-39
| MATERIALS | US regulation39 | EU regulation and provision | Chinese regulation38 |
|---|---|---|---|
| Plastics, resins, additives, polymerization aids | 1340 food contact notifications + GRAS and prior sanctioned substances (Title 21 CFR Parts 175, 177, 178) | 843 in the EU positive list37 including 428 with SML or SML group, and 587 additives | 339 in positive list 86 with SML/QM or SML group |
| Rubber | 176 substances in the French positive list 40 | 88 substances 23 with SML/QM | |
| Printing inks | 5104 substances (IAS) in EuPIA guidance41 and Swiss Ordinance42. For NIAS, see43 | 97 substances 33 with SML/QM | |
| Paper and board (including recycled) | 482 substances (Title 21 CFR Part 176) | 1556 substances additives in Council of Europe resolutions 44 and good manufacturing practices 45. For recycled materials, see 46, 47 | 277 substances 77 with SML/QM |
| Compliance testing by modeling | Yes (plastics) | Yes (restricted to plastics) | No restriction on applicable materials |
| Risk Assessment including migration modeling | Broad range of applications in petitions in relation with consumer exposure determination | Broad range of applications in petitions in relation with an upper estimation of consumer exposure | Not applicable in petitions |
GRAS = generally recognized as safe; SML: specific migration limit (maximum concentration in food); QM: quantity maximum (maximum amount in the material before contact); IAS: intentionally added substances; NIAS: non-intentionally added substances.
A crisis occurs when a substance not authorized is found in the packaging material or when the levels in food raise concern due to its ubiquitous distribution or due to significant exposure of specific or global populations. As an illustration, the substances from materials intended to be in contact with food and exceeding EU migration tolerances during the period 2002-2018 are listed in Figure 3 in decreasing order of occurrence. Half of the 1956 cases are associated with imported tableware and with contaminations by heavy metals. Packaging alone represent less than 6% of the total with lids involved in 45% of cases. The main crises associated with packaging materials and their likely causes and consequences are reviewed in Table 2.
Table 2. Analysis of the major crisis involving food contact materials
| Crisis (class) | Period (key references) | Cause | Consequence |
|---|---|---|---|
| Levels of plasticizers from PVC cling films above 100 mg**⋅kg-1** | 198x 48-53 | Widely used as additives (plasticizer, solvent) with large amounts, not covalently bonded to the material backbone | Restrictions or ban of many phthalates in FCM applications |
| High levels BADGE and of its reaction products of BADGE from can coatings | 1997-today 54 | starting substance for the manufacture of epoxy resins, used as an additive, functioning as a stabilizer and as a plasticizer à reaction with medium in contact | TDI 0.15 mg/kg b.w (BADGE) SML 1 mg/kg of food (reaction products) |
| Primary aromatic amines from agglomerated cork stoppers | 2000-today 55, 56 | Surface treatment, adhesive, lubricant à reaction products | SML 0.01 mg:kg of food applied to the sum of PAA released (annex II of 37) |
| Primary aromatic amines from laminates | 2000-today 57-59 | polyurethane adhesive à reaction due to thermal treatment | SML 0.01 mg/kg of food applied to the sum of PAA released (annex II of 37) |
| High levels of epoxidized soybean oils | 1988 – today 60 | Large amounts in PVC plasticized, high lipid solubility, long time storage | Lowering of SML to 30 mg/kg for infant food |
| High levels Nonyl-phenols | 2004-today 61 | Breakdown product of tris(nonylphenyl)phosphite (authorized in EU 10/2011) | strictly limited by Directive 2003/53/EC 62 restriction REACH annex XVII 63 |
| Semicarbazide leached from the thermal decomposition of azodicarboamide from gaskets used in baby food jar closure technology (press twist and twist-off lids) | 2003-2005 64, 65 | Breakdown product of azodicarbonamide during the heat treatment | ban 66 |
| ITX | 2005-today 67 | Bad identification of transfer/contamination paths from ink to foodstuffs Bad information exchange between stakeholders in supply chain | No regulated in plastic material regulation REACH study |
| Benzophenones from printing inks | 1995-today 68 | Bad identification of transfer/contamination paths Bad information exchange between stakeholders in supply chain | SML: 0.6 mg/kg |
| Bisphenol A leached from Baby Bottles | 2004-today 69, 70 | Widely used in infant products | Lowering of SML to 0.05 mg/kg Replaced by other substances New risk assessment ongoing by EFSA |
| Ubiquitous contamination by mineral oils from recycled papers and boards | 1993-today 71, 72 | Recycled paperboard, difficult in analytical analysis | Proposition of SML of 0.5 mg/kg |
The inset of Figure 3 and Table 2 would suggest that the number of contamination cases would increase with time. The better effort of authorities to identify, track and contain the contamination by FCM led to more frequent reporting. Regardless of the real risks, the successive crises can coatings, bisphenol A and mineral oils increased the awareness of the general population and, in return, promoted the sake of different management strategies and better integration along the supply chain.
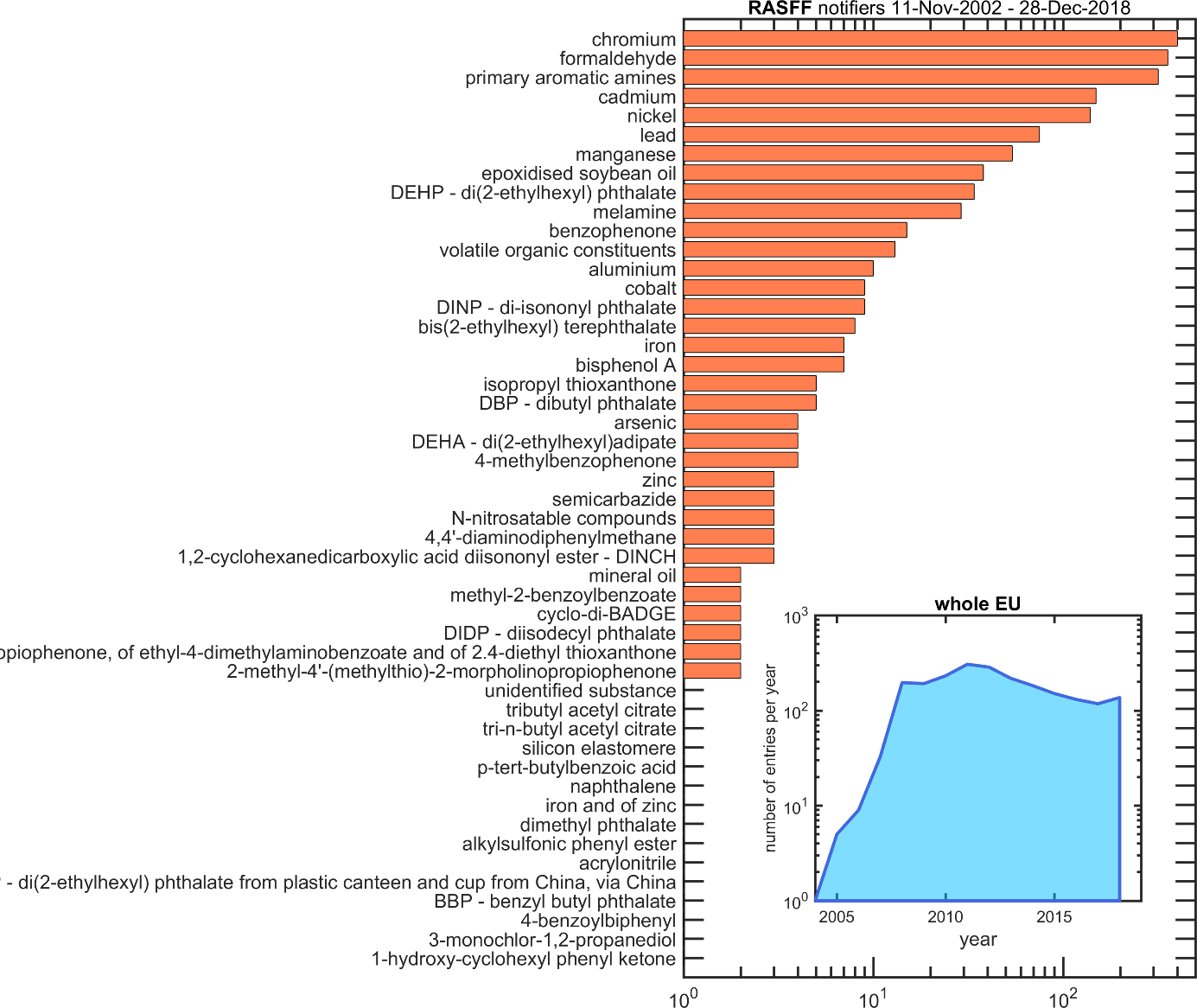
Figure 3. List of contaminants from food contact materials reported in the European Rapid Alert System for Food and Feed73 (extraction on Dec 31st, 2018). The inset shows the evolution with time of the number of alerts issued by all member states, corresponding during the period 2002-2018 to 955 border rejections, 459 alerts, 288 information for attention, 284 information and 216 information for follow-up.
4 Risk assessment for decision making
Highlights on modeling, risk assessment, and decision making
- Migration modeling is a cognitive process aiming at capturing the essential mass transfer phenomena responsible for the contamination of food by substances originating from materials.
- Calculations are carried out in a way that they guarantee they are more severe than real conditions.
- Only compliance can be demonstrated by calculations and simulations.
- Calculations are in essence different than accelerated tests and should be used to reproduce real but conservative contact conditions (time, temperature, interactions with food).
- Sophistications in calculations require to be introduced progressively and in a comprehensive manner starting from the most conservative (severe) conditions.
- Variability and uncertainty must be characterized and documented.
- The whole process can be integrated into preventive approaches (safe-by-design) or stochastic calculations (see section 7)
4.1 Overview of migration modeling
4.1.1 What is currently permitted?
Notwithstanding the introduction of accelerated tests for compliance testing, simplified alternatives to traditional migration testing were sought in the nineties. The common interests of the industry and the authorities were summarized by Begley 74, “Traditionally, migration tests are performed by using food-simulating liquids such as water, edible oils, ethanol/water solutions and sometimes food. These tests are time-consuming in two ways; generally, the accelerated tests run for at least ten days, and the analysis of the migrants at low concentrations in the simulants or food is generally difficult. These analyses are also expensive and generate hazardous laboratory waste”. Migration modeling was proposed both in the US (earlier works 75 ) and in EU (earlier works 76-79) to tailor the process of migration assessment. Migration modeling is nowadays mostly extended in EU via a specific task force TF-MATHMOD publishing updated guidance 80 Migration modeling is broadly accepted for compliance testing 37 and risk assessment (see 81) of food contact materials with the following strict restrictions:
- estimated values – whatever the calculation procedure and underlying assumptions – must be at least as severe as the real test and overestimate the migration;
- calculations cannot be used to demonstrate the non-compliance.
Similar methodologies are used by the industry to calculate the level of decontamination (cleaning) of materials in mechanical recycling processes. But in this case, the amount released by the material should be estimated accurately and not overestimated. Additionally, it is worth noticing that the state of polymers is very different between the conditions met by the consumer (moderated temperatures) and the industrial conditions of recycling (high temperature, solvent-swollen). Only mechanistic modeling can cover both cases. Modeling is not restricted to any material (thermoplastic, thermoset, paper, and board), but it has been tested chiefly for thermoplastics and with non-uniform coverage.
There is no limit to the scope of modeling in current regulations and practices. Compliance testing can be seen as the simplest usage of modeling and validating a closed loop of recycling as the most complex application (see Figure 1). Repeated use, composite materials and safe-by-design approaches can be envisioned of intermediate complexity. All applications (small and large) obey in fact to same global scheme, where the result obtained at the scale immediately below is used at the upper scale, as shown in Figure 4, The complexity of modeling relies on the number of scales considered and not on the system (film, bottle, etc.) subjected to the modeling activity. The keys to identifying the number of scales, components and steps are discussed all along the chapter.
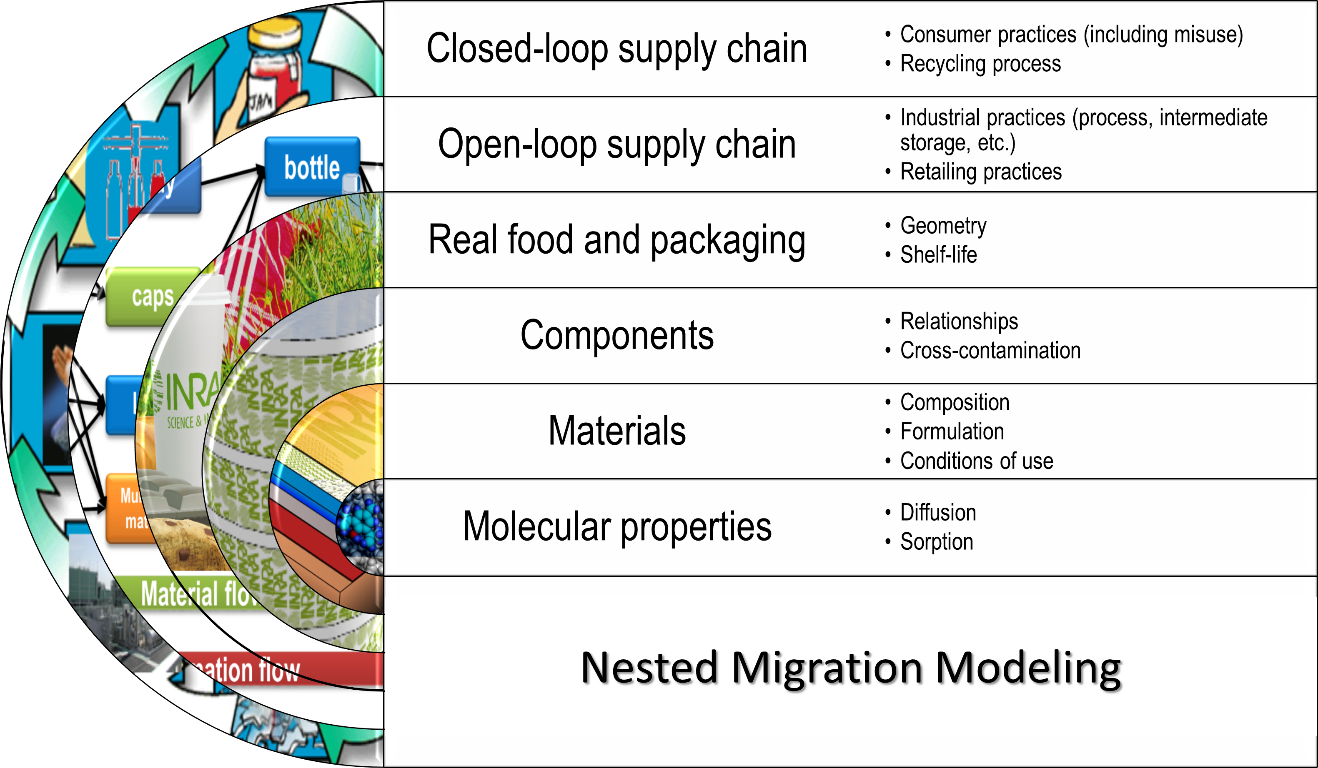
Figure 4. Overview of the nested modeling strategy to predict migration for all applications depicted in Figure 1.
4.1.2 Modeling using a tiered approach: from worst-case scenarios to detailed conservative ones
The exact value of the contamination of the food is never achievable because the conditions of contact are variable (time, temperature) between comparable products and because our knowledge of molecular mechanisms is perfectible. As a result, the practice seeks successive approximations of the migration in a tiered approach, as shown in Figure 5. At the first tier, the estimation is very coarse and connected with the highest overestimation factor. If the determined concentration at tier is higher than the threshold of concern, the next tier is triggered by introducing substantial refinements and details, and so on. The process stops when no additional information can be introduced (experiments need to be preferred) or when the calculated concentration is lower than the threshold of concern. The lowest tier within the threshold of concern defines the proper level of knowledge required to demonstrate compliance or to guarantee the safe use of a material, substance, or process. There is no systematic procedure to identify the minimum tier to reach the goal, and only the needed information can be listed.
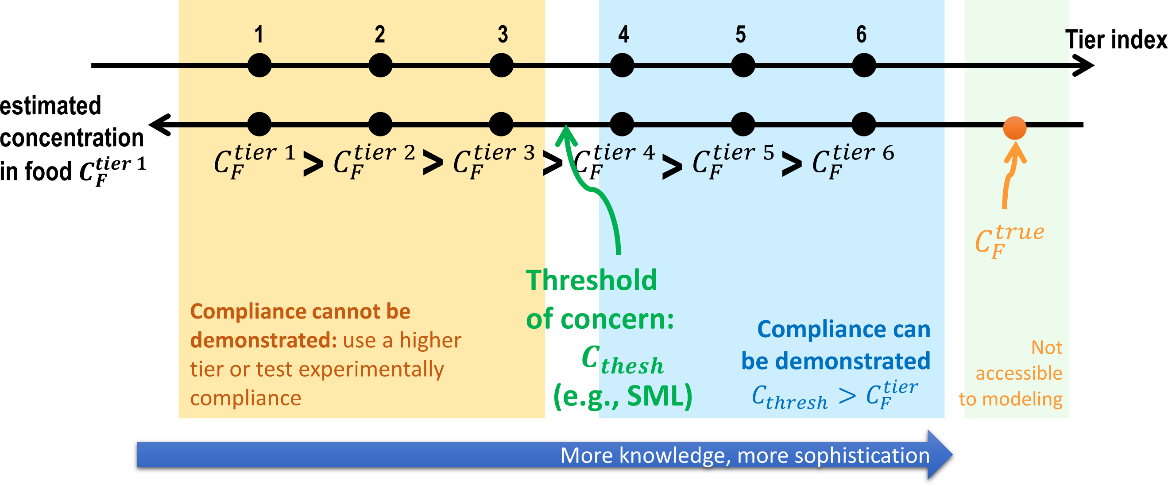
Figure 5. Principle of the tiered approach to demonstrate compliance for food contact materials. Compliance is demonstrated as soon as the estimated concentration is greater than the threshold of concern. Tier 1 is usually associated with total migration (see Eq. ).
The possibilities and prerequisites for using modeling in compliance testing are reviewed in Table 3. The mentioned tiers , and * are indicative and corresponded to a modeling level more sophisticated than the first tier. The first tier is usually coined to “total migration” and corresponds to the total transfer of substances into food (see Figure 13). The corresponding concentration in food, , is determined by a “dilution” model:
where is the initial concentration in the material (regardless its distribution) expressed in mass per volume (preferred in this work) or in mass per mass (industrial practice). is the material-to-food volume or mass ratio. When one-dimensional representations are used, is also the ratio between the thickness of packaging walls, denoted , and the characteristic dimension of the food, denoted , where is the effective surface area in contact, counting usually the total surface area in contact with the food and the headspace. By contrast, the food volume is restricted to the condensed part of the food (solid or liquid).
Table 3. Prerequisites to use calculations as an alternative to migration testing.
| Prerequisites | Type of estimate | Examples of works | tier† |
|---|---|---|---|
| Migration modeling or related calculations | lectures , reference text books (specific or general) | Lectures on migration 82-84, text books on migration 85-90 ; reviews and case studies on migration modeling 86, 89, 91-95 96-98 ; reference text books on packaging90, 99; reference text books on mass transfer100-107 | R1 R2 R2 R3 R3 R3 |
| Identity of material | technical specifications, recycling code, measurements | supplier, regulation, standard 108, 109, FTIR spectra | R1 R2 R3 |
| Characteristics of the polymer | density , glass transition temperature , crystallinity | supplier; handbooks110, 111; measurements | R1 R2 R3 |
| Identity of the substance | real substance , chemical structure, chemical descriptors | supplier; deformulation 112 and/or spectroscopy 113, 114; analoguous substance | R1 R2 R3 |
| Packaging geometry | 1 kg packed in 6 dm2 , 1D approximation of real geometry, 3D real geometry | regulation; supplier, end-user; research work111, 115-118 | R2 R2 R3 |
| Contact conditions (time, temperature, phase in contact…) | standard test conditions , accelerated conditions, real conditions | end-user; regulation | R1 R2 |
| Initial concentration | real values, overestimates | supplier; guidance, orientation formulabrute force deformulation 113, 114 | R1 R2 R3 |
| Diffusion coefficients (see §**5)** | real values, overestimates, molecular theory, molecular modeling | measurements, literature 119-130 Piringer model131 or equivalent 100; free-volume theories and their extensions123, 124, 126, 132-136 ; Molecular Dynamics simulation 137-142 | R1 R2 R3 R3 R3 R3 |
| Partition coefficients or sorption isotherms (see §**6)** | real values, overestimates, molecular theory, molecular modeling (Flory Approximation), molecular modeling | measurements, literature; guidance 143; Kirkwood-Buff theory 144 ; Flory -Huggins theory145-148; solubility parameters 110, 112, 149, 150 ; theory of interacting liquids151; thermodynamic integration, insertion method 152-157 at atomistic scale; atomistic calculations within the Flory approximation112, 113, 158-164 | R1 R2 R3 R3 R3 R3 R3 R3 |
| Mass transfer resistance in the contacting phase (see §**4.2.3.4)** | none, correlation diffusion coefficient, flow | worst-case; liquid or gas model 100, 101, 103-105, 165-167; Graetz type problem; full simulation coupling168 | R1 R2 R2 R3 |
| Acceptable thresholds (see §**8.4.1)** | 37-39, 37, 38, 169-174, threshold of regulation175 , 176 | Regulations; regulation policy 74 ; recommendations (GMP), literature | R1 R2 R3 |
†Recommended for compliance testing at the first (), second () and third () tier. If the value of the migration is larger at the second tier than at the first one, use the second tier. If the value of the migration is larger at the third tier than at the second one, use the third one. =*specific migration limit; =maximum amounts; = threshold of toxicological concern; =good manufacturing practices. and maximum concentration in food are related as , with and the food and packaging volume respectively, the density of the polymer and the partition coefficient.
4.1.3 Key steps in migration modeling and risk assessment approaches
Any migration modeling for compliance testing, risk assessment, and safe-by-design approaches should be initiated by the review of five important sections with an intent of providing an inventory on:
- the formulation of materials (intentionally-added or not substances),
- the components included in the design;
- the steps followed by the material, the finished packaging, and the packaged food;
- the information obtained from suppliers, regulations, industrial recommendations;
- the described mechanisms of contamination.
For each section, the items need to be ranked and prioritized according to their suspected or foreseen importance on the contamination of the packaged food, as shown in Figure 6. The principles and illustrations described in this chapter can be used to extend the systems, steps, substances,… under scrutiny beyond primary food packaging and contact layers.

Figure 6. Generic steps to review in migration modeling and safe-by design approaches. The depicted example corresponds to the review for a new aseptic carton packaging for milk to be consumed by infants.
4.2 Migration modeling for compliance testing and beyond
In agreement with EU recommendations 80, this section details the assumptions and conditions suitable for compliance testing at high tiers using a comprehensive description of mass transfer. The levels of description would correspond to tiers and in Table 3.
4.2.1 Principles of migration modeling
Highlights on the principles of migration modeling.
- Migration obey simply speaking to the well-known laws of diffusion.
- The mass transfer from one material to another material, or the food requires specific treatment and attention as it is not implemented by default generic numerical software (commercial or not).
- One-dimensional mass transfer calculations are sufficient for most of the applications if mass balances are well preserved.
- The cost of modeling is dramatically reduced by simulating the contacting phase implicitly with proper boundary conditions. It is important to note that the substances within any eventual mass transfer boundary layer are not included in the food mass balance when implicit models are used.
- Beyond its obvious numerical advantages (abacuses, master curves, pre-tabulated results), dimensionless formulations based on similitude principles facilitate the review of model assumptions and results.
Substances non-covalently bound to the polymer are subjected to thermal agitation, which causes in return a random translation of their center-of-mass. Each additive, monomer, residue jumps or walks randomly in the polymer matrix from one accessible void to the next one. The substances reach the interface eventually with the food, where the same hopping process is repeated usually at a higher pace. When volatile substances meet a gas phase, their skew trajectories are governed by the collision with gas molecules. In all cases, random walks occur in three-dimensions, but a concentration gradient develops only at leaching interfaces, in its perpendicular direction. As the walls of the packaging are thin compared to the characteristic food dimension, migration can be approximated as a one-dimensional mass transfer problem as shown in Figure 7. The migrating substances are depicted either as individual molecules or solutes (i.e., scales are not respected) showing microscopic concentration fluctuations or as smooth macroscopic concentration profiles (continuous lines). Different symbols are used whether the solutes are in the polymer (position ); in a small boundary layer in the food and of thickness , where a concentration gradient exists (position ); or in the food bulk () without any significant concentration gradient (e.g., assumption of a perfectly mixed medium). Choosing as a free parameter enables to cover almost all contacting phases (gas, liquid food or simulant, solid and semi-solid food) with reasonable complexity.
Figure 7 plots simulation results using the concepts of statistical physics (i.e., the molecules jump randomly vertically and horizontally without “knowing” where the interface is located) and by using the concept of continuum mechanics (i.e., balance on populations and macroscopic fluxes on elementary volumes). The stochastic and deterministic point of views are equivalent and highlight that the observed macroscopic gradients are the consequence of the evolution of the distributions of solutes with time and not its cause. In the upward direction, the random displacements are compensated by the same and opposite microscopic flux in the downward direction. The net balance is zero, and no concentration gradient can develop. The substances translate at the same frequency in the horizontal direction (i.e., isotropic diffusion), but since no solute comes to compensate the flux from left to right at the beginning of the contact, a net flux develops from left to right, resulting in the spreading of a concentration gradient from the source (the polymer: ) to the food (the food: ). Statistical physics and continuum mechanics counts molecules in a very similar fashion, via the concepts of probability density, and of volume concentration , respectively. is the total number of migrating substances in the whole system and the number of molecules in an elemental volume . The concentration at the interface between F and P (denoted P-F) requires specific treatment and analysis. Since the principle zero of thermodynamics does not hold for mass transfer, both density and concentration are discontinuous at the P-F interface. If no reaction occurs at the interface, the mass balance is kept across the interface (i.e., no substance is lost). Additionally, the principle of microscopic reversibility entails that the amount of substances crossing the interface per time unit from left to right (denoted P→F) is exactly matched by the amount of substances crossing the interface in the opposite direction (denoted F→P). In other words, any substance located exactly at the interface has the same probability to go in P and F, irrespectively its origin. This principle of microscopic mass balance reads:
where is the frequency of translating from the compartment A to the compartment . The concept of local chemical equilibrium developed among others by Henry Eyring provides a robust framework to express the frequencies of passage from one state to another one without justifying the details on how the change in conformations and local velocities affect the passage from A to B. The frequency of passage is written as:
with the free energy associated to the transition state and the free energy of sorption of the solute in A. The preexponential factor is independent of temperature; its expression depends on the statistical ensemble used to express probabilities. By combining Eqs and , the molecules distribute across the interface with a ratio of probabilities equal to:
where and indicate the position and time; the food-packaging interface is located at . The concentration profiles are, hence, continuous across the P-F interface only when the free sorption energies are similar in both compartments. In the general case, the concentration profile is discontinuous across the interface. Figure 7 plots cases for an apparent partition coefficient of 0.5. In other words, the substance has a twice more chemical affinity for P than for F, as expected for plastic additives and monomers. For conservative migration modeling, values of higher than unity are preferred to maximize the gradient and consequently the amount transferred to the food. When the release of substance does not modify the properties of the polymer (polymer densification, a shift of the glass transition temperature ), the ratio of concentrations is likely to be constant at the interface.
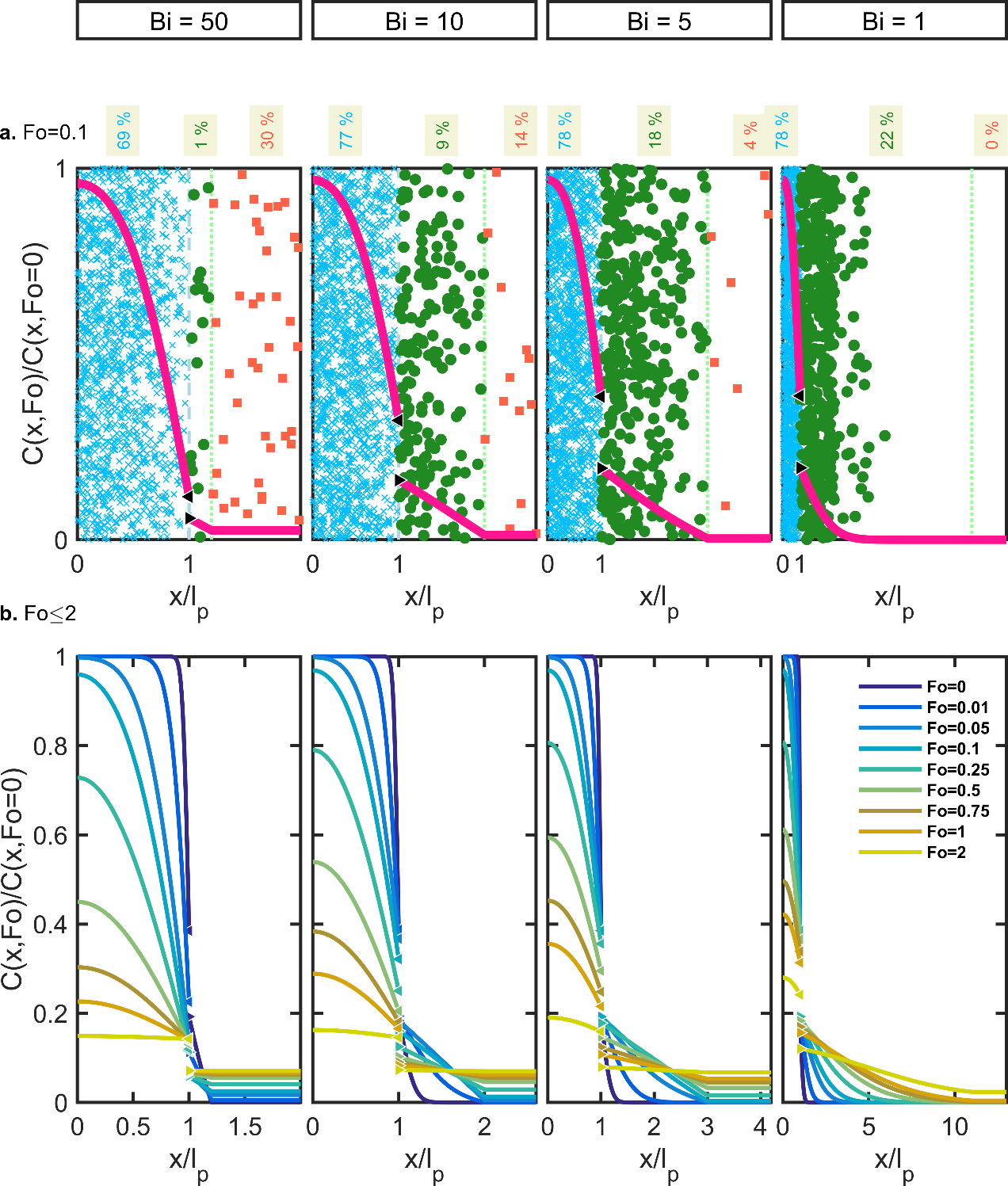
Figure 7. One-dimensional description of solute diffusion (e.g., additive, monomer) from the packaging wall (position: , individual solutes identified as ×) to the contacting phase (individual solutes identified as ■) via the food boundary layer (individual solutes identified as ●): (a) random distribution of solutes and corresponding concentration profile at and (b) after contact times up to . The percentages in the top part represent the residual amount in each compartment.
4.2.1.2 Migration modeling and similitude properties
Under the assumption of uniform and constant transport and thermodynamic properties in each compartment (polymer: P, boundary layer: BL, bulk contacting phase or food: F), the mass transfer problem is self-similar according to a small number of dimensionless parameters or ratios. According to the principle of similitude, a real problem can be compared to a theoretical case without dimensions if all independent dimensionless quantities are similar. The key dimensionless quantities are reviewed in Table 4.
Table 4. Key dimensionless quantities of the migration from monomaterials. Contact is assumed to be initiated at .
| Dimensionless quantity | Meaning | Justification |
|---|---|---|
| Dimensionless concentration | is a reference concentration, usually the initial concentration in the polymer . | |
| it is defined from Eq.. (4) | Partition coefficient | At macroscopic equilibrium, it is also defined as with and the volume-averaged concentrations in F and P, respectively. |
| Dimensionless position | is characteristic food dimension, usually the thickness or the ratio if the geometry is complex, with the volume of the material and the surface area in contact with . It is recommended to maximize by also including the headspace in the calculations of . | |
| Dimensionless time | is the diffusion coefficient in the polymer at the temperature of contact. The integral form needs to be preferred if the diffusion coefficient is variable with time (temperature change) | |
| or | mass Biot or Sherwood number | where is the thickness of the boundary layer and the diffusion coefficient in F, such that is the effective mass transfer coefficient across the boundary. |
| Dilution ratio | This number is defined as the ratio of characteristic lengths and controls how the substances are diluted in the food, usually much larger than the packaging. |
4.2.1.3 Explicit vs implicit food representation
It would be logical that migration models describe, how the migrants distribute in the food explicitly. Solid foods, such as a chicken or a pizza, are not expected to have all parts contaminated similarly. For risk assessment, we consider that all parts are intended to be ingested, including the most contaminated sauce in contact with the packaging. As a result, only a global estimate of the food contamination is required, as measured with a liquid simulating the entire food. Replacing a solid by a liquid or vice-versa has a consequence on the rates of mass transfer. This part discusses the differences between explicit and implicit representations of the food and of the risk to underestimate the real migration.
Figure 7 represents explicitly mass transfer in the food, that is the concentration profiles in the food are also calculated. The depicted cases correspond to a characteristic food length of (i.e., thin food to make the boundary layer visible). The total domain has a length of . When the food is represented explicitly, the amount transferred to the food is defined as:
Eq.(6) accumulates substances in the boundary layer (round symbols) and in the food bulk (square symbols). Implicit food representation will describe mass transfer only in the packaging and apply a proper boundary condition between the food and the packaging at the position . With the help of Eq. , the flux at the interface, denoted , can be expressed only with concentrations taken inside the packaging or in the food far from the interface, .This assumption open the way of an implicit representation of the food via a boundary condition relating the diffusion at the packaging-food interface with the flux entering into the food:
Eq. (6) offers a good approximation of the explicit representation when the contact time is sufficient to reach a fully developed concentration profile (linear, so-called Prandtl approximation) inside the boundary layer. The critical Fourier number is given by . The profile plotted in fFigure 7a for and deviates from the assumption above. The critical Fourier number is, indeed, of 1.67 and the value of is close to zero, whereas the food is already contaminated via its boundary layer. Implicit food representation approximates the concentration in the food, , by its concentration far from the interface. By noticing that the flux is taken after the boundary layer, one gets:
For and if the threshold of concern is not too low, the amount present in the boundary layer can be neglected (less than 1% in Figure 7a when ) and an implicit representation can be used. Its main advantage is the dramatic reduction of the problem complexity and of the computational time. In very thin or low barrier films and in solid foods, the implicit food representation may underestimate the contamination of the food severely. The amounts in the boundary layer reported in Figure 7a reach 9%, 18% and 22% for = 10, 5, 1 respectively. When an implicit representation is used, calculating the concentration in the food from the mass balance in the packaging between and does not solve the issue as the closure equalities are enforced at any time:
The amount present in the boundary layer is always neglected in migration representing the food implicitly. Only by choosing artificially as a worst-case scenario makes this amount negligible at the price of migration much faster than the one expected in the real conditions.
4.2.1.4 Other assumptions
We describe in this section the constitutive equations to describe mass transfer from monolayer and multilayer materials, when the food is represented implicitly via the boundary condition and the food mass balance (8). The total packaging thickness is denoted for a packaging (e.g. laminate) consisting of layers. At the position (usually the surface exposed to the ambiance), an impervious boundary layer is assumed so that the amount transferred to the food is maximized. All substances are assumed to be well dispersed where they have been incorporated (e.g., no blooming effect) and below their concentration at saturation (i.e., no supersaturation).
4.2.2 Governing equations for monolayer materials
4.2.2.1 Overview
The full set of equations for monolayer materials including the initial condition (IC), the transport equation (TE), the boundary conditions (BC) and the mass balance on the food compartment (MB) reads:
where is an exponent controlling the system of coordinates ( : Cartesian, : cylindrical; : spherical); is the diffusion coefficient possibly variable with concentration (e.g., case of plasticizers used at high concentrations).
When the diffusion coefficient in the packaging is considered constant along with , Table 4 and system 9-13 yield the following dimensionless formulation for Cartesian coordinates:
When , the third type boundary condition at (Robin boundary condition) can be replaced by a simple coupling with the mass balance. By differentiating BM respectively to , one gets:
The worst-case scenario, and corresponds to the Dirichlet boundary condition .
4.2.2.2 Concentration in the contact phase at thermodynamical equilibrium
According to Eqs. , the maximum concentration in food is obtained at thermodynamical equilibrium ( ):
In practice it is convenient to express the kinetics of desorption in food as a function of the fraction of the equilibrium value:
4.2.2.3 Dimensionless migration kinetics and their analytical approximations
The dimensionless migration kinetics are plotted in Figure 8. The analytical solution associated with the Dirichlet condition is given by Eq. 4.18 in Crank’s book 102 and reads :
For small values, the approximation requires to be very large (103 or 104) and a more efficient approximation can be obtained by combining an approximation of Eq 4.20 in Crank’s book 102 with Eq. for as:
Approximations and are plotted along with the results of numerical simulations in Figure 8. The common assumption of the linearity of with is well verified while and when the equivalent length of the contacting phase and are large. At intermediate values, the Dirichlet condition offers a conservative approximation (i.e., is overestimated) and Eq. can be used safely for compliance testing. However, when (e.g., small food volume, low chemical affinity for the food), Eq. must be avoided due to a significant risk of underestimation of low values. The equilibrium is, indeed, reached much faster due to a much smaller amount to transfer and because the concentration at the F-P interface never vanishes. An accurate estimation of migration requires ad-hoc numerical solutions or special analytical solutions. In mathematical terms, finite volume effects cause the propagation of shockwaves between the polymer and the contacting phase: the addition of substances to F modifies instantaneously the capacity of P to transfer additional substances, and so on for the next substances creating positive and destructive interference across the mass transfer boundary layer when it exists. One practical consequence is that analytical solutions are without closed-forms and therefore more complex than Eq. XXX.
- For and , the analytical solution verifying finite volume effects and boundary condition is given by Eq. 4. 37 in Crank’s book 102 and is very accurate at a reasonable cost for .
- For arbitrary and values, new solutions verifying the general boundary condition (see Refs. 127, 177-179). Short-time and long-time solutions were optimized for efficiency and to integrate more complex physics such as non-linear sorption isotherms or for boundary conditions variable in time.
The general solutions are not detailed here as their expressions exceed the scope of the article. When , the Eq. 4. 37 in Crank’s book 102 reads:
The zeros of the transcendental equation, , increase with and also when decreases. This behavior demonstrates that converges exponentially and more rapidly to equilibrium whenvalues are low. The linearization with ceases to be correct earlier and is associated to slopes varying with . As the values of are usually not tabulated beyond in reference text books (see Table 4.1, p. 379 in 102, it is recommended to restrict the use of Eq. XXXX to .
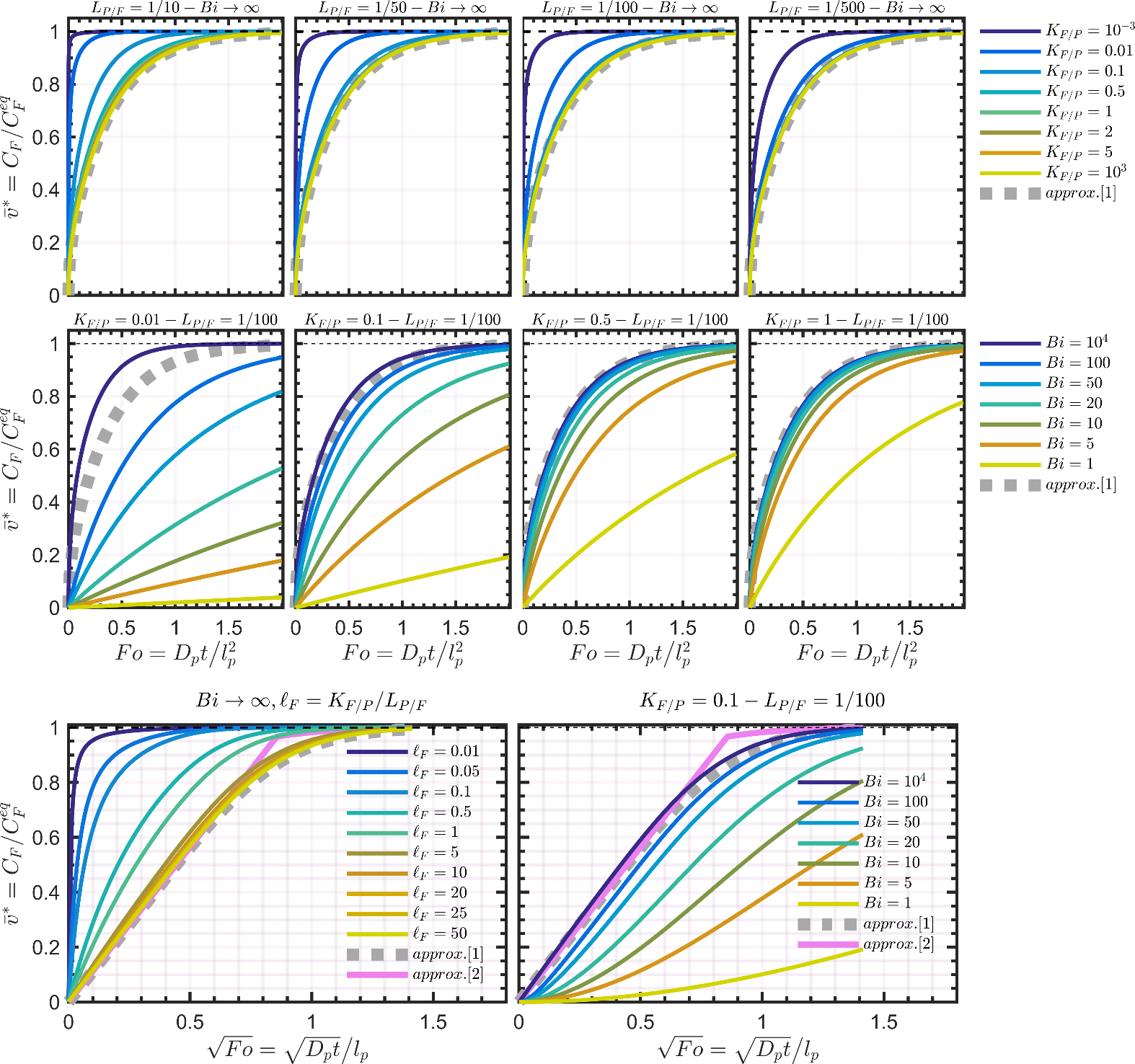
Figure 8. Dimensionless desorption kinetics for various values of , and with . Approximations [1] and [2] are given by Eqs. XXX and XXX , respectively.
4.2.3 Governing equations for multilayers
Highlights for multilayers
- Multilayer can be seen as a generalization of monolayer materials but with additional features such as functional barriers (delayed migration) and reservoir layers (accumulation inside one or several internal virgin layers).
- When the partition coefficients between layers and their diffusion coefficients are constant with time, the total migration is the sum of the migrations associated with the contribution of individual layers.
- Uncertainty in partitioning and the initial distribution of migrants can be overcome by moving “artificially” the content on one layer to a layer closer to the contacting phase.
- The calculation procedures presented in this section have been introduced in the guidance to EU Regulation 10/2011/EC.
4.2.3.1 Thermodynamical assumptions The case of materials consisting of materials or layers ( ) can be seen as a generalization of the monolayer case ( ) at the expense of a few additional assumptions and conventions. Because monolayer systems were dominating in the 20th century, the reasoning supporting US and EU regulations was, hence, devised based on an assumption of a migration without delay and obeying to a scaling proportional to the square root of time. The conventional condition of ten days at 40°C was thus thought to be equivalent to a test of one hundred days with a factor comprised between unity (equilibrium) and (. Moving the substances away from the P-F interface delays substantially the mass transfer to the contacting phase. This behavior is central to the concept of functional barrier 180; it was initially explored to promote the incorporation of recycled material – possibly contaminated due to post-consumer misuse or mixing with non-food grade materials – in co-extrudates. The recycled polymer is sandwiched within two layers of virgin polymers. Similar problems can be resolved only by adapting the initial condition in the equation system (9) to the need instead of using a uniform distribution. When the materials are different in nature, a contact condition similar to Eq. (4) needs to be considered. The proposed description relies on an assumption of a linear and reversible sorption of substances in each layer so that a linear sorption isotherm is assumed in any layer, including in the food. By denoting the partial pressure of the migrating substance, the isotherm associated to the Henri constant reads for each layer:
(17) With a sake of generalization, the layers including the food are indexed from (food: F) to (layer the most distant to F), with being the contact layer, as shown in Figure 9. The residual concentration in each layer is for and .
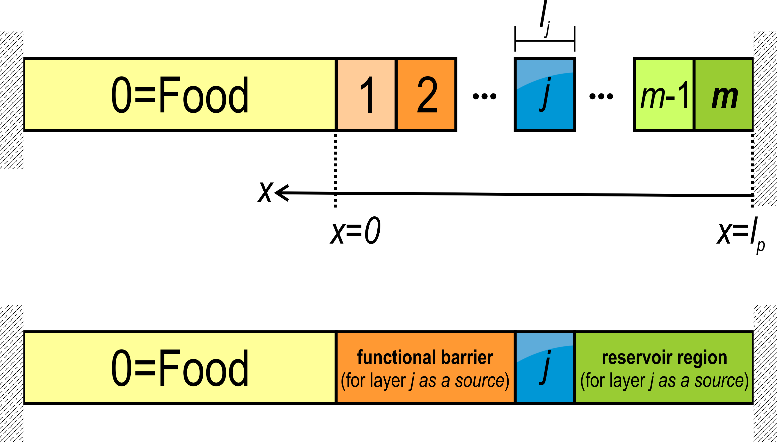
Figure 9. Indexing rule of a material including m layers (total thickness ) in contact with a food product indexed 0. The left and right external boundaries are considered impervious (no mass loss). The concepts of “functional barrier” are “reservoir” assume that the layer j is the source (with non-zero initial concentration). It is used in §4.2.3.5 and §4.2.3.6.
4.2.3.2 Concentration in the contact phase at thermodynamical equilibrium
The Henri isotherm defined in Eq. (17) offers a robust but simplified thermodynamic representation of the variation of the chemical potential with the local composition in the system. The validity of the model and its generalization are discussed in §6.2 . Partial pressure [p\left( x,t \right)] is a continuous potential, and thermodynamical equilibrium is achieved when its value is uniform across the structure. By neglecting mass losses, Eq. (17) and the mass balance between and enables to generalizes Eq. (12):
(18) where is the partition coefficient between the layer and the food.
4.2.3.3 Transport equations
Transport equations are unchanged and are piecewise-defined:
(19) and connected at internal interfaces via the double conditions of mass conservation and local thermodynamical equilibrium:
(20)
4.2.3.4 Limiting mass transfer resistance
A dimensionless formulation of Eqs (6), (19) and (20) is achievable at the expense of choosing a reference layer, , setting the reference time scale . In numerical algorithms, where stability and convergence are very stringent, it is convenient to choose as a reference layer, the layer associated to the highest mass transfer resistance (lowest permeability) is the best choice:
(21) If several conditions need to be compared, a natural choice is to choose the contact layer as the reference layer ().
4.2.3.5 Typologies of migration behaviors
The main behaviors, which can be observed with multilayers, are illustrated in simple configurations corresponding to a bilayer structure (each layer has a thickness ) in contact with a liquid phase with a characteristic thickness and associated to . The five considered cases are summarized in Table 5 and were associated with a similar initial amount and comparable final concentration in the contacting phase ca. . The other parameters were , , and the time scale . The calculated profiles and kinetics corresponding to the five scenarios are plotted in Figure 10.
Table 5. Illustration of the main behaviors associated with multilayer structures. The concepts of functional barrier and reservoir are illustrated in Figure 9.
| interpretation | code | ||||
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | uniform distribution (equivalent to a monolayer) | [1,1]×[1,1] |
| 0 | 2 | 1 | 1 | functional barrier (barrier to diffusion only) | [0,2]×[1,1] |
| 2 | 0 | 1 | 1 | reservoir layer (same capacity) | [2,0]×[1,1] |
| 0 | 2 | 2 | 1 | functional barrier (barrier to diffusion and of solubility) | [0,2]×[2,1] |
| 2 | 0 | 1 | 2 | reservoir layer (twice less capacity) | [2,0]×[1,2] |
Monolayers and functional barriers lead to uniformly decreasing concentration profiles. The corresponding desorption kinetics in F are respectively proportional to the square-root of time and proportional to time after some lag time equal to . For the same initial amount in the structure and after the lag time, the functional barrier ceases to operate and leads to a migration proportional to . Only a functional barrier combining a diffusion barrier ( ) and solubility one ( ) can slow down the desorption durably. Reservoirs behave very differently; they are associated with non-monotonous concentration profiles, accelerated desorption kinetics while converging to a very similar concentration at equilibrium. For the same initial content and when the barrier on the right is higher than the barrier on the left , the “reservoir” configuration overestimates the migration kinetics associated with all other configurations.
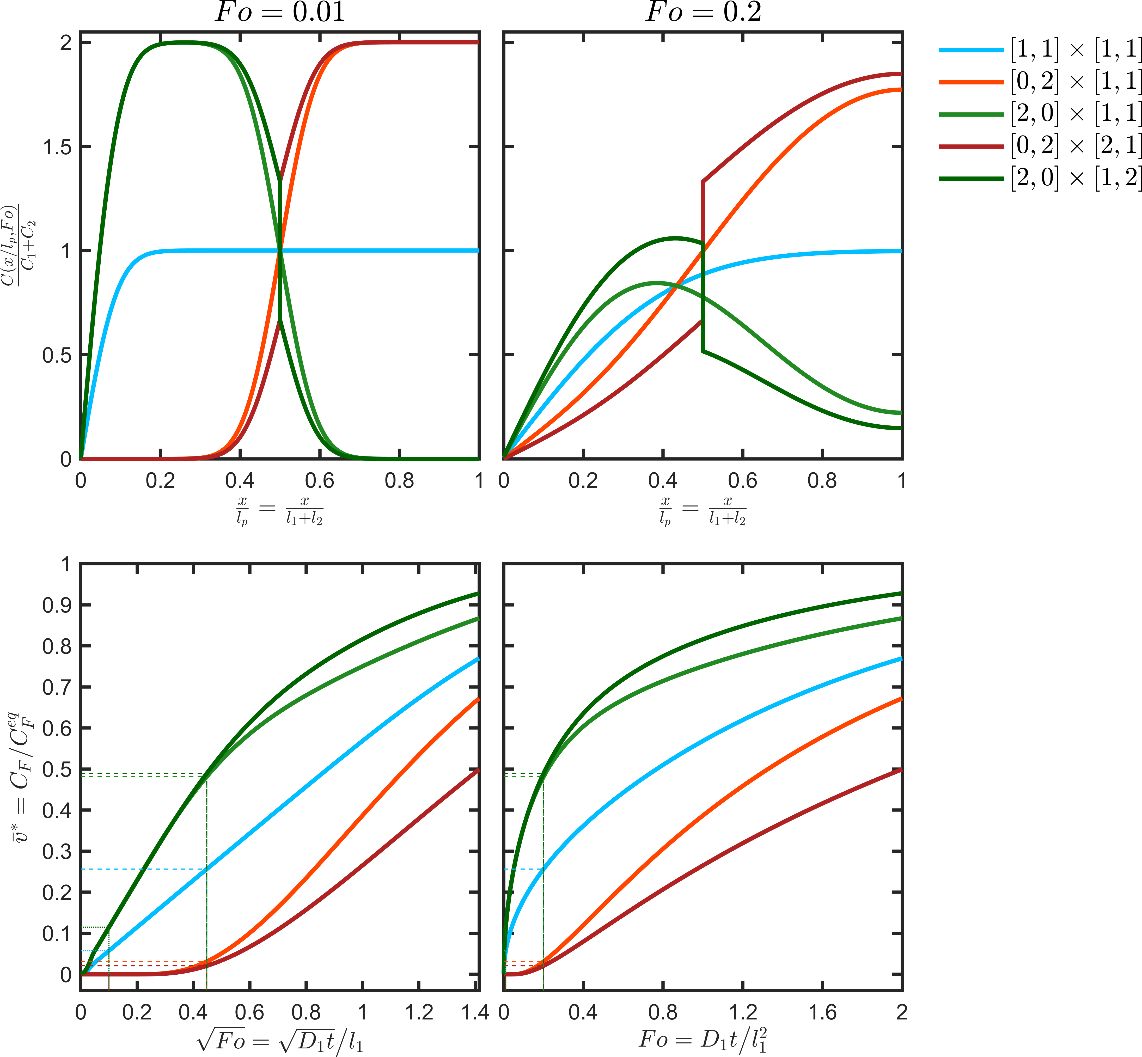
Figure 10. Concentration profiles (top) and migration kinetics (bottom) for the bilayer structure and scenarios detailed in Table 5.
4.2.3.6 Superposition principles and conservative scenarios for multilayer and multicomponent systems
Mathematical principles
Multilayer structures offer a broad range of behaviors. In the simplest cases, as shown in Figure 10, desorption kinetics are monotonous with time. It may be not the case if the functional barrier and reservoir effects are combined. The calculations for complex multilayer are complicated by the difficulty to associate the uncertainty in diffusion and sorption properties on the concentration in food. For monolayer materials, a conservative scenario is achieved by overestimating simultaneously , and . For multilayer materials, no similar rule holds. Intuitively based on the illustrated configurations in Figure 10, it can be stated that for the capacity of the layer to transfer its content, (amount transferred to F at the time ), is maximized (denoted ) if the following properties are fulfilled:
Conditions have a mathematical justification in the linear properties of the equations -. The solution of any linear decomposition of the initial concentration profile is equal to the sum of the individual solutions:
Example for a trilayer material ABC
Eq. XXX is particularly significant as it is valid for any partitioning of the source terms in the material, respecting or not the positions of the layers. An application of the additivity ofvalues (concentration profiles and kinetics) is shown in Figure 11 for a trilayer structure ABC detailed in Table 6.
Table 6. Parameters used to construct realistic and conservative migration scenarios depicted in Figure 11 and Figure 12. Quantities are expressed respectively to the likely values† for the first layer (the three layers ABC are indexed 1,2,3). They are scalar when the contribution of each layer as a source is considered in combination with others (the three sources are considered at once). The contributions of individual sources are indicated by 3×1 vectors mentioning the properties of all layers considered as a source or not.
| property | case-study (likely) contribution of the jth layer | conservative scenario (high tier) contribution of the jth layer | worst-case scenario (low tier) contribution of the jth layer | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.5 | 0.3 | 0.2 | 0.5 | 0.3 | 0.2 | 0.5 | none | |
| 1 | 1 | 1 | [1,0,0] | [0,1,0] | [0,0,1] | 3.5 | 0.6 | none | |
| 1 | 1 | 1 | [1,10-3,10-3] | [1,1,10-3] | [1,10,10] | 1 | 1 | none | |
| 0.3 | 0.8 | 2.0 | [10,10,10] | [1,10,10] | [1,1,10] | 10 | 10 | none |
†Likely value = true value or close to the true value in the considered scenario.
The simulation of each layer individually underlines the different mechanisms controlling the contribution of each layer: reservoir effect for source A (scaling of desorption kinetics with the square root of time) and functional barriers for B and C (desorption kinetics linear with time after significant lag-times). The depicted profiles are assumed to the “likely” or “true” ones. They are considered inaccessible to simulation and should be approximated at some tier in a way that the concentration in F is always overestimated (see Figure 13).
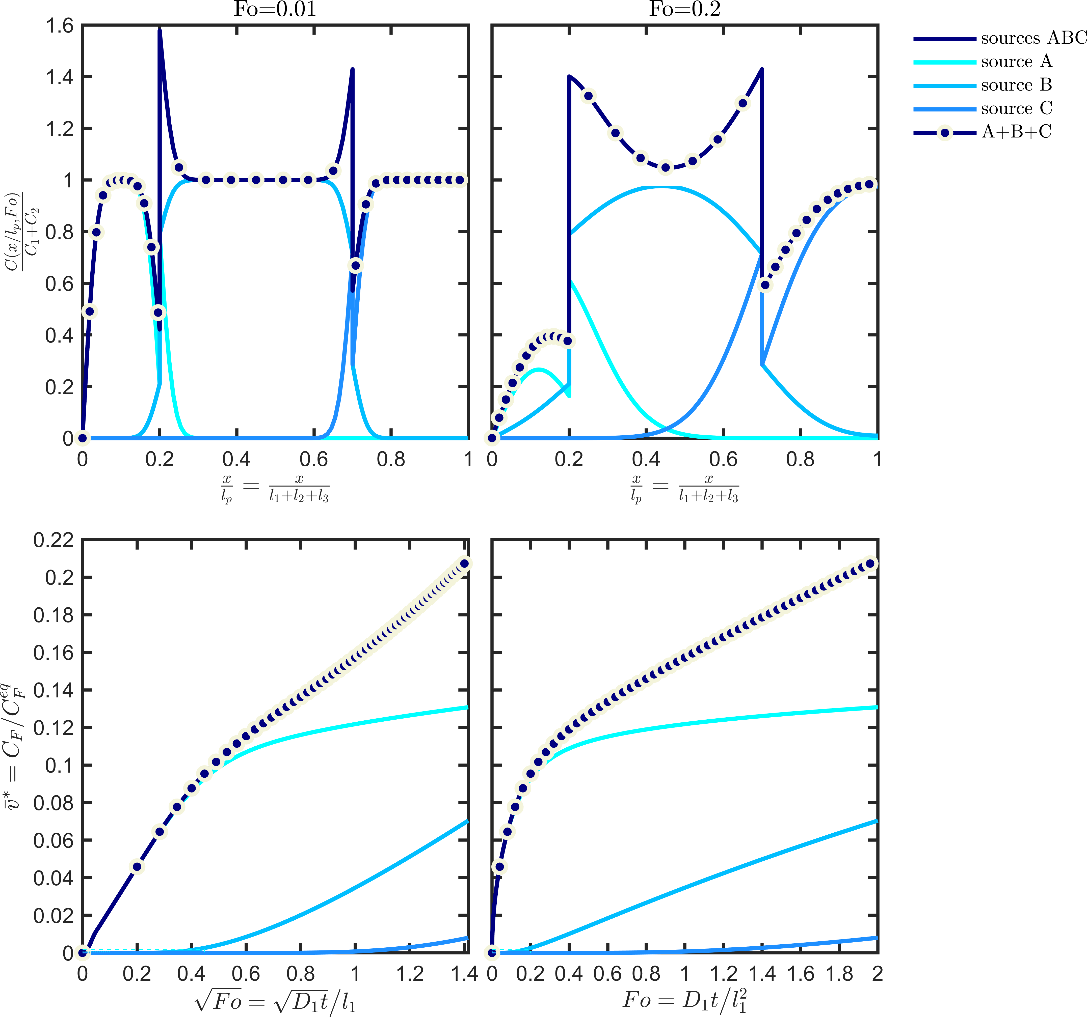
Figure 11. Illustration of the additivity of the sources (see Eq. ) for a trilayer structure ABC associated with the case study detailed in Table 6: concentration profiles (top), kinetics (bottom). The case “sources ABC” is obtained by simulating the whole structure. The result A+B+C corresponds to the mathematical addition of the contributions of the three sources.
Eq. XXX provides a numerical procedure to devise conservative scenarios for multilayer structures. A similar procedure has been detailed in the section 4.2 of the European guidance document 143. We repeat here the procedure for the sole overestimation of the chemical affinity effects and by keeping the diffusion coefficients to their “likely” values. The core idea is to prevent or hinder the diffusion of the substances in the jth layer to the right (by assuming that the food is on the left) and to facilitate their desorption to the left, to bring the contaminants closer to the food. The “conservative scenario” of Table 6 applies a factor ten to the Henry-like coefficient(s) of the source and behind. The likely and values are kept for the layers between the food and the jth layer. To prevent back diffusion in the reservoir layers the diffusion coefficients were divided arbitrarily by a factor 103. The corresponding kinetics are shown in Figure 12, with their parameters listed in the section “conservative scenario” of Table 6. The diffusion coefficients towards the food are overestimated by a factor 10. At intermediate Fourier numbers below 0.4, the kinetics is not significantly overestimated, but a significant conservatism is achieved at larger Fourier numbers when the overall migration is controlled by the second and the third layers as sources. This case study demonstrates how migration scenarios can be finely tuned to decrease the uncertainty related to the behavior of internal layers. The contact layer as a source can always be considered as a single monolayer.
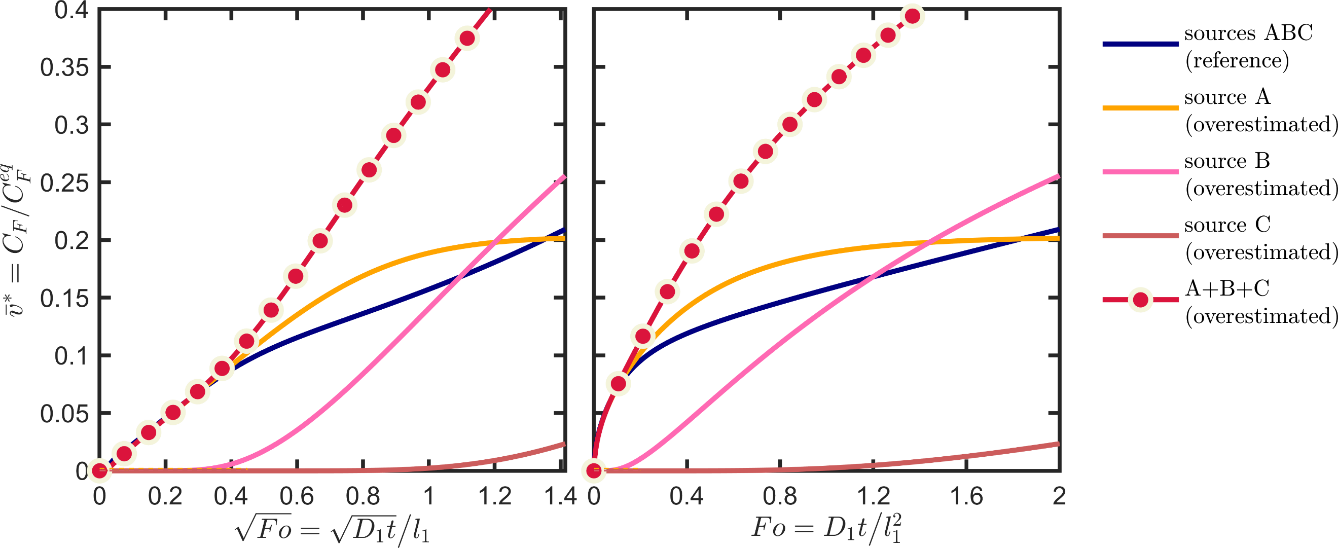
Figure 12. Illustration of the conservative scenario of Table 6 based on the overestimation of the contribution of each source. The reference corresponds to the initial case-study configuration also depicted in Figure 11.
In practice, any uncertainty on the internal partitioning between layer can be converted into a conservative scenario by forcing mass transfer to the food and by relocating “artificially” the content from the layer to layer . The iterative procedure is illustrated in Figure 13 and can be applied iteratively to decrease a -layer problem into a , , etc. layer problem, until to reach tier 1 (total migration). The first iteration applied to the case-study is denoted “worst-case” scenario in Table 6. The procedure may overestimate dramatically the real migration, but it keeps the applicability of conservative calculations to demonstrate safety at low cost. For risk assessment, the procedure may be applied with caution as it may lead to unrealistic consumer exposure.
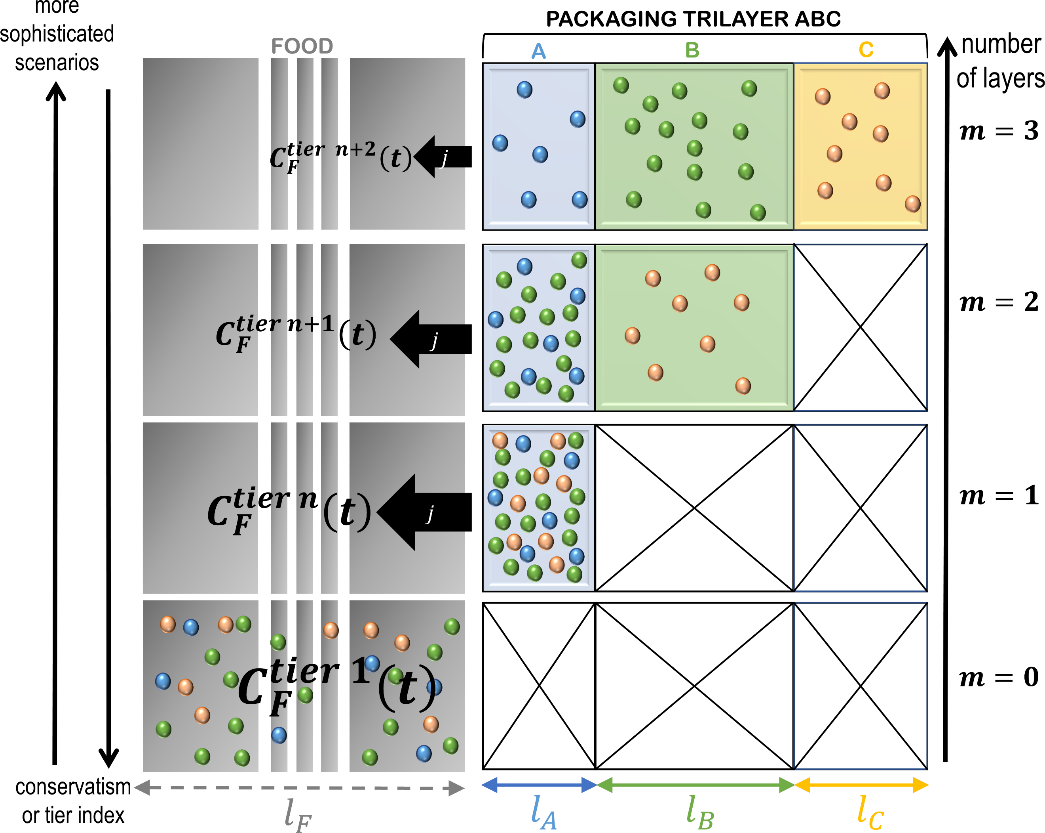
Figure 13. Principles of the simplification of a -layer problem (here ) into a problem with a lower number of layers and, therefore, easier parameterization. The represented distributions in the packaging corresponds to initial conditions at various tiers.
4.2.4 Strategies and equations to simulate multiple steps and conditions
This part discusses the invariance of migration estimates, namely , with the order of contact and thermodynamical conditions met by the components of the packaging before and during food contact.
Highlights on the strategies to simulate multiple steps and variable conditions.
- The initial dispersion of the substances between materials and the subsequent migration into the contact phase requires at least a two-step modeling and simulation.
- Temperature and relative humidity are variable during storage, transportation, etc. and subjected to uncontrolled diurnal and seasonal variations. Their variations can be integrated in chained simulations (one condition = one step), where the outputs calculated at the previous step are used as inputs at the next steps.
- Chained scenarios can be factorized under certain conditions in a shorter series of conditions without respecting the original order of steps or variations.
- Factorization keeps unchanged migration results only if the contact conditions are unchanged and if apparent partition coefficients are independent of temperature.
- Factorization should be avoided if the dispersion in food plays a significant role and in the presence of polar migrants.
- Factorized scenarios offer practical estimates for repeated uses.
- Probabilistic migration modeling (see §7) can be used to analyze the effects of known and unknown variations.
4.2.4.1 Problem formulation
Mass transfer between components and materials occur insidiously along the supply chain. Figure 14 illustrates conditions triggering or altering migration from printed materials. Many uncontrolled factors may affect the extent of mass transfer: i) variable contact or exposure times, ii) random combinations of storage and transportation steps for intermediate, finished packaging materials and packaged foods, iii) changes in temperature and relative humidity (e.g., seasonal, diurnal, international transportation), iv) modifications of boundary conditions during any stage of materials lifetime and product shelf-life. The redistribution of migrants between materials, layers, and components deserve special attention as it remains usually ignored by end-users. In practice, cross-contamination occurrences can be also considered indirectly (i.e., without causaility) as impurities and non-intentionally added substances. Without being exhaustive, cross-contamination is highly likely from cured adhesives and printing inks, from recycled materials and any material with rich volatile organic compounds. Packaging and materials stored in stacks and reels ease cross contaminations by contacting internal and external layers, regardless the presence of a functional barrier (absolute such as a metallic layer or relative such as barrier polymer) in the structure. Due to periodic conditions, the inner layer can act as a reservoir of contaminants before the food is put in contact.

Figure 14. Illustration of the redistribution of the migrants from UV-cured printing ink and their subsequent migration in food for long shelf-life products. The depicted cases cover hot-filled products (e.g., soups, pasteurized juices, sterilized dairy products), dry or ready-to-eat products stored in cardboard boxes.
From a mathematical point, the succession of steps and temperature variations can be seen as a sequence of constant conditions occurring in variable order. In the presence of conditions occurring at the time , the composite solution is obtained by integrating the coupled system via the Chasles’ relation:
The determinations of the duration of each step and their corresponding temperatures are critical. Representing all diurnal and seasonal temperature variations shown on the timeline of Figure 14 would require 2×450=900 successive simulations (one every 12 hours). On the one hand, a rigorous approach suggests that the congruence of all the steps should be strictly preserved to get reliable conclusions. In this case, how to identify the worst-case combination of conditions or steps? If the temperature variations are uncontrolled, how to build a conservative sequence? On the other hand, a naïve approach would suggest that the times series in Eq. XXX could be built from mutually independent steps assembled as the sum of a series of standard and well-controlled steps (e.g., cold, moderate and warm days), and one series and of stochastic contributions, representing an extra safety margin.
4.2.4.2 A first intuitive approach
The variations of between steps are not factorizable but the dimensionless times are. Their effects are additive and commutative (see Eq. XXX for the demonstration). If the diffusion coefficient is the only quantity varying with temperature and the plasticizer content (i.e., no change in the partitioning, and the packaging dimensions), the effects of is captured via the generalized Fourier number:
where is the diffusion coefficient of the most limiting material, component or layer, and the one-dimensional equivalent thickness (see Eq. to identify ).
Eq. XXX is equivalent to the low of the composition of velocities along a curvilinear coordinate system tangent to the trajectory going from A ( ) to B (). The analogy between spatial translation along a winding road and the translation along the curve vs. is illustrated in Figure 15 by comparing the travel via three modes of transport (each of duration at a speed: ) with the cumulated contamination after three steps (of duration at temperature . The total distance is , and the cumulated migration is independently on the order of the steps. Replacing the physical time by a cumulant measuring the total arc-length of the curve or the road makes it possible to use endpoint estimates (one simulation) instead of chained simulations ( simulations). In this new space, the residence times – represented by the density of markers on the curves – are not uniform. They are distributed more densely at departure and destination, but more sparsely in the middle region has the studied system follows different routes.
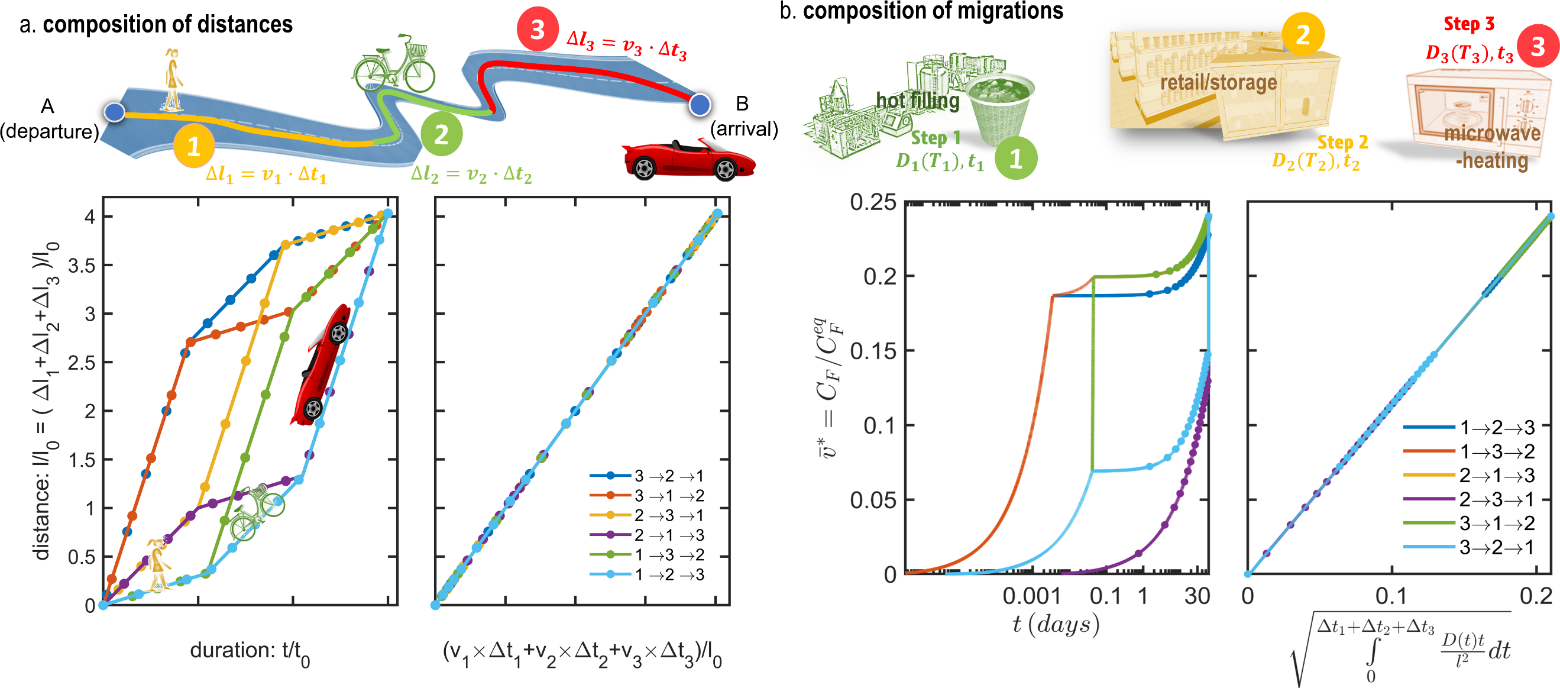
Figure 15. Illustration of the composition rules (a) for distances and (b) for the migration from a monolayer material, and of their invariance with the order of the steps (see Eqs. and ).
Eq. XXX suffers, however, a lack of generality as it applies only to the limiting mass transfer resistance and not to all layers. As a rule of thumb, It offers an acceptable if the function is monotone with (i.e., when . A simple counter-example can be, however, constructed by noticing that the concentration at equilibrium depends only on the initial and final states, but not on intermediate steps.
The conditions of exchangeability of steps (which is more generic than Eq. ) is discussed hereafter in more general terms. Two conditions are analyzed: i) when the effect of the mass transfer resistance is considered (explicit representation) and when the number of molecules does not change, and ii) when an implicit food representation is used (i.e., Eqs. XXX,XXX and XXX). The distinction between explicit and implicit food representation is relevant, as the boundary layer delays the effects of perturbations and may contain a significant amount of contaminants, which are ignored at low values in implicit representations (see §4.2.1.3).
4.2.4.3 Strict conditions of exchangeability with explicit food models
Microscopic description of the random walk of molecules between P and F
The visited distance by a deterministic system is and is invariant with the order of visits. At microscopic scale (i.e., at a scale where they can be separated), the trajectories of migrants in materials and the food verify this property (distances are additives), but with a different relationship with time (displacements are proportional with time). The random displacements of additives and residues shares, instead, notable features with random walks and continuous stochastic paths. In a loose sense, substances jump randomly at discrete times (random walks) or as continuous events (stochastic paths). Their skewed trajectories are nowhere differentiable, and velocities cannot be defined in a classical sense. Under a hypothesis of stationarity of the microscopic random process (the quantity has the same statistics as for any ), we will justify a law of composition for the mean-square-distances, denoted , visited by the molecules: = . is mathematically defined as , where is the average distance (first moment) and the square distance to the food-packaging interface located at:
The one-dimensional space approximation with explicit food representation is defined on the domain so that the probability density verifies: and for or . A differential form of the growth of with time is inferred from a special case of the Fokker-Planck equation (similar to Eq. XXX). By multiplying both sides by and by integrating over the entire domain, one gets:
with and being the diffusion coefficients in P and F, respectively. The left-hand side is equivalent to . The right-hand side requires two successive integration by parts along with the impervious boundary conditions at and , and the conservation of the flux at . The simplifications associated with the compact support of leads to:
For any initial distribution of substances (single molecule or collection of molecules), Eq. describes the evolution of the mean-square distance to the FP interface. Since equations do not include any thermodynamical consideration (Eq. was not enforced), Eq. is valid while (beyond this length scale, finite size effects dominate and ). It shows that increases as , when the concentration in F () is low. When the amount of substances in F becomes larger and because the molecules diffuse faster in F than in P, increases more rapidly. is the effective diffusion coefficient between P and F when both materials are replaced by an equivalent medium. A version similar to Eq.XX for a homogeneous medium and known as Einstein equation is presented in §5.1.1 (see Eq. XXX).
Condition of invariance of the dispersion of solutes with the properties of the contacting phase
Eq. XXX shows that the composition is independent of and of the amount already transferred to the food only if the inequality is verified. The dispersion of contaminants is, hence, independent of the order of variations of with time when:
By noticing that is the total migration (see Eq. ) and that the diffusion in polymers is 1:100 or less lower than in the food one, we see that the invariance with the order of the steps hold only at the beginning of the migration process or when the chemical affinity for the food is very low. Eq. could be justified with the example of a large food volume submitted to a cold condition during , denoted followed by a warm condition during the same time, denoted with . The normal order would lead to a small mass transfer during and a very strong during . Performing the transfer in the reverse order will cause even a higher mass transfer during the first step. If the food is large, the extra number of molecules transferred to the food during the first step will not have enough time to be transferred back to the packaging. As the food-packaging contact is not symmetric and , the two orders might not lead to similar irreversible behaviors: the food is contaminated in both cases but not in the same extent.
Discussion on the limits introduced by implicit models
The fundamental results exposed here rely on an explicit representation of the food, where molecules displace at a finite velocity. This subtle detail is not reproduced in implicit representations, which assume a perfect mixing outside the mass transfer boundary layer (the velocity of molecules). Only a delay is considered in the boundary assuming a linear profile instead of a parabolic one (see the distribution of molecules depicted in green symbols Figure 7). The next paragraph reviews the conditions of commutativity of implicit models under variable conditions. The condition of commutativity is less severe as the back flux from the contacted phase is immediately compensated in the numerical scheme. But as shown here, the condition of commutativity is expected to be verified in real life, only when the condition is met. The equivalence between time and temperature is acceptable only far from the equilibrium ( ), but it is unacceptable closer to equilibrium ( ), where the effective mass transfer is governed by effective partition coefficient across the P-F interface. From Eq. X, partitioning coefficients are independent of the temperature only if the difference of free sorption energies between P and F are kept constant () when the temperature is raised.
4.2.4.4 Conditions of exchangeability in food implicit models
Overview of implicit numerical models and their solutions**
Food implicit models are by far the most used. They are more flexible to accommodate variable conditions and chained conditions. They have been implemented with various numerical models using different spatial discretization schemes. The finite difference method is the dominant approach in one-dimension problems, but it loses accuracy at interfaces when large jumps in concentrations and diffusion coefficients occur. The finite element method is the standard in the industry as it enables to integrate any partial differential equation system on arbitrary geometrical domains, using a grid approximation (consisting of triangles, quadrangles, curvilinear polygons). The finite volume method is in essence similar (values are calculated on a meshed geometry), but the equations are integrated on small, but not infinitesimal, volumes. By positioning the interface between volumes at the exact location, where thermodynamic constraints such as Eq. XXX needs to be strictly verified, the method enables to maintain exact mass balances and the continuity of chemical potentials between materials. The pros and cons of each method are discussed in Ref.181. The three methods can be put in a matrix form, coding for a system of ordinary differential equation:
The common practice is to include the concentration in P discretized and the concentration in F in . Since the food is represented implicitly, one node is sufficient for the food and is a vector mapping its continuous version. is a triband matrix for discretization scheme at order 1 and pentaband matrix for quadratic finite elements techniques.
When the transport and thermodynamic properties are constant, the solution of Eq. XXX respectively to the initial condition is , with .
Composition rules when chained simulations are used (example with three steps)
The solution of the mass transfer associated with three conditions: , with the stiffness matrix for the ith step (e.g., coding the effect of temperature on diffusion and partition coefficients) reads:
The steps are exchangeable if the equality satisfies also:
which is verified only if and commutes (meaning that for ).
Conditions of exchangeability imposed by the physical-chemistry
Reference 181 demonstrated that a necessary and sufficient condition to have the solution applicable is that the ratios of Henry coefficients (see their definitions in Eq. XXX) remain constant with time between all considered steps. As a result, adding or removing a material/layer/food (i.e., changing from to 0 or the reverse) breaks the condition of exchangeability of steps. The condition of exchangeability is also likely to be lost for polar solutes dispersed between polar and apolar phases. As shown in §6.2.2 (see Eq. XXX at infinite dilution when ), the excess enthalpies of mixing are negative for the firsts indeed and positive for the lasts. In this particular case, the apparent activation energy of the partition coefficient between and is maximal, and the effect of temperature needs to be simulated by respecting the order of the temperature variations (i.e., by using Eq. XXX of Eq. XXX). For apolar solutes, the activation of is, conversely, almost compensated by a symmetric variation of , when the temperature is changed.
4.2.5 Discussion on the choice of accelerated conditions and the identification of critical steps
Highlights for multiple steps and variable conditions
- Accelerated conditions and time-temperature relationships need to be verified according to the rules of factorization mentioned in §4.2.4.
- The contribution of any step or component by obtained by difference if the comparison includes all steps and components.
- Probabilistic migration modeling (see section 7) can be used to evaluate the safety margin associated with accelerated and equivalent conditions.
4.2.5.1 Factors of acceleration and possible biases.
The different theoretical developments presented in this part highlighted the complications to reach exact modeling of migration for a given product. The real contact conditions and couple time×temperature need to be considered and incorporated in a proper simulation scenario. Subtle variations of temperature and contact times may modify the estimates. We remember the reader that a tiered approach, as shown in Figure 5 is always preferable. A robust approach to assess the effects of various sources of variability (e.g., temperature variations) and uncertainty (e.g., effects of temperature of diffusion and partition coefficients) is presented in §7. Probabilistic modeling applied to Eq. XXX can be used to derive conservative estimates either with a prescribed risk or with a prescribed safety margin (see. Figure 23).
Accelerated tests are used experimentally to reproduce the level of contamination after the end of the food product shelf-life while using much shorter contact times. By assuming that migration is controlled by one single mass transfer resistance (index ), the principle relies on replacing the real condition by the accelerated condition . When amount transferred at equilibrium is not affected by temperature (see. §6.2.2 for discussion), the ratio of values between accelerated and real conditions read:
where is the apparent activation energy of the diffusion. This parameter is critical and will be discussed in §5.4. For monolayer materials, an activation energy of 60 kJ⋅mol-1 yields an activation factor of ca. 5 when the temperature is raised to 40°C from 20°C. Testing food packaging at 40°C during ten days is equivalent to a test of 50 days at 20°C. If the shelf-life is of 100 days, the risk of underestimation of the true migration can reach up to factor . In the presence of a functional barrier, the factor of underestimation can be even larger as shown in Figure 10.
4.2.5.2 Causality, critical steps, and crtical components.
In the presence of multiple steps, it is recommended to perform a test, which mimics the most critical steps for the final value of . Due to the lack of generality of Eqs. XXX and XXX, the factorization strategies should be avoided to identify critical steps. The reference 181 demonstrated that the contribution of one single step, denoted , or of one component (label, cap, film, bottle, etc.), denoted , could always be determined by difference as:
where represents the sequence including all steps except the step ; including all components except the component .
The contributions of the sum of all steps and components are larger than the real contamination. This behavior is expected as several steps can lead to similar effects. Corollary, Eq. XXX enables the identification of steps, which occur without contact with food (see Figure 14) or of any component, even if there is no direct or intended contact with food. When the contributions are normalized by a threshold of concern, , they can be used to seek the likely causes (industrial practices or components) which lead or which could lead to exceeding tolerances. The effects can be cumulated over several substances to get a global criticality of the step or the component of interest. This procedure has been used as the foundation of a preventive approach of mass transfer reusing the principles of the methodology FMECA (Failure Mode Effects and Criticality Analysis) 181. The approach can be employed to analyze an entire supply chain or industrial practices, as illustrated in Figure 13. The assessment of the risk of cross-contamination of the constituents of UV-cured printing ink during the long-term storage of pots in stacks is shown in Figure 16. The stacking step is indexed 1. The redistribution of contaminants triggers contamination immediately during and after filling the pot at 80°C. Migrants accumulates continuously in the food during storage until the final consumption. By difference, the contribution of the first step can be evaluated. After normalization by , it is demonstrated that the first step provides the largest contribution to the risk of exceeding the legal limit.
Figure 16. Contribution of the stacking of pots before filling them at hot temperatures with a Chinese soup along the supply chain: a. steps of supply chain; b. assessment of a severity of a single step; c. comparison of a several step. After ref. 181.
5 Diffusion properties in polymers
Highlights on the diffusion coefficients in polymers (thermoplastics, thermosets, elastomers)
- Diffusion coefficients are essential properties to evaluate the performances of functional barriers and to assess the kinetics of migration in food.
- Diffusion coefficients are strongly affected by the size of migrants: volume effects dominate for bulk and rigid solutes (e.g., aromatic solutes), the number of rigid sub-units dominates in flexible solutes.
- The activation of diffusion follows an Arrhenius relationship only far from the glass transition temperature ( ). Near , free-volume effects dominate, and apparent activation energies depend on both temperature and the size of diffusants.
- For compliance testing, it is recommended to use overestimates of diffusion coefficients to reduce the risk of underestimation of migration.
- When modeling is used to validate mechanical recycling processes of polymers, it is recommended to use either realistic estimates or probabilistic modeling (see section 7).
5.1 Definitions of diffusion coefficients
Diffusion coefficients in the polymer, , are essential properties to calculate migration according to Eqs. and . Reference textbooks [see chapter 11 of Ref.102, see Ref.107 proposed several definitions of diffusion coefficients including overestimates (see chapters in Ref.89). We review in this section the definitions, which are relevant in macroscopic migration models and which are capable of incorporating the effects of the molecular structure of the migrants and the polymer.
5.1.1 Self- and trace-diffusion coefficients
As a starting point, it is worth noticing that the random walk of migrants (without gradient) does not occur in an empty space but among other molecules (polymer segments and other solutes, such as plasticizers). By reusing the illustrations of Figure 7, the net flux density perpendicular to a cross section located at a position is proportional to the difference of the net velocities between the solutes (i.e., molecules of the migrant of interest), and the Stokesian velocity of the surrounding molecules :
In the limit case where the migrant is of the same nature as the surrounding molecules (e.g., pure liquid plasticizers, pure solvents), , there is no net flux () and no macroscopic gradient . The diffusion coefficient is still defined, and it is called the self-diffusion coefficient but not correlated to any macroscopic gradients.
The opposite limiting case corresponding to infinite dilution ( ) and a solid behavior ( ) also leads to an extremely low net flux (), but with a concentration gradient. The corresponding diffusion coefficient is called trace diffusion coefficient. Experimentally, the velocity can be determined from the lag-time, , associated with the migration across a functional barrier of thickness . By noticing that (see §4.2.3.5), one gets
Eq. XXX is correct but suffer a lack of generality for an arbitrary initial distribution of solutes. The approach presented in §4.2.4.3 is more general. Eq associated to shows that:
Factor 6 appears in Eqs. XXX-XXX instead of factor 2 shown in Eq , because the random walks are considered in three dimensions and not anymore in one dimension. The mean-square-displacement is calculated accordingly from the 3D positions of the center-of-mas of all migrants, and averaged over all possible initial positions . The definition is used to calculate diffusion coefficients by molecular dynamics simulations in polymers 140, 182. In practice and to remove any uncontrolled drift (*i.e.,* ) due to the displacement of surrounding molecules, the positions are not absolute but taken respectively to the center-of-mass of the whole system.
5.1.2 Mutual diffusion coefficients
Section 5.1.1 describes diffusion either in a stream or when there is only one diffusing species. Diffusion in a medium with variable composition generates fluctuations in (see Eq. ) and change the nature of the interactions with the surrounding molecules. The picture is complete if we also consider the point of view of the surrounding molecules, whose diffusion is also affected. An example could be the diffusion of antioxidant (or any large molecule) in a heterogeneously plasticized polymer (i.e., see Ref. 183), where the local mobility of the antioxidant is strongly enhanced by the local amount of plasticizer in the ternary system (migrant+plasticizer+polymer). Similarly, the diffusion of the plasticizer increases the mobility of polymer segments. Strictly speaking, all these effects cannot be described by the sole shift of the glass transition temperature and the increase of free volumes presented in §5.3 (see also discussion in chapters 5 and 6 of the reference textbook 107). As the diffusion of one species affects the diffusion of all other species and reciprocally, self- and trace diffusion coefficients cannot be used. The correct description requires the use of the Onsager’s theory and generalized forces. The entire system (polymer+solutes) reorganizes to minimize its total free-energy. A cationic surfactant will, for example, accumulate at the surface of the material to minimize its interaction with the polymer. A poorly soluble colorant or pigment will do the same at high concentration. The resulting concentration profiles evolve therefore spontaneously from an initial uniform distribution after processing to a highly heterogeneous one. Such evolutions with matter moving from low to high concentrated regions cannot be predicted with concentration gradients as effective driving forces. The gradients of chemical potentials need to be used as an effective driving force. In the sake of simplicity and to avoid a tensor definition of the diffusion coefficient, we consider only the effect of the chemical potential of the migrant, denoted , as driving force. Rigorously, a linear relationship should be considered between the flux of the migrating substance and the driving forces associated with all species in the mixture. The generalized driving force, , induced by the local variation of the chemical potential of the migrant in the mixture reads:
where is a friction coefficient; is the chemical potential of the migrant defined respectively to its volume fraction and activity coefficient . The relationship between the gradient of chemical potential and the concentration gradient is given by:
with being the thermodynamical factor depending on the composition, whose dependence with concentration can be determined from the expression of the sorption isotherm see §6.2). An effective diffusion coefficient, , related to the flux is identified from Eqs. XXX and XXX as:
where subscripts trace and mutual refer to the value of the property at infinite dilution and in mixture, respectively. For binary solvent-polymer mixtures, Vrentas and Vrentas 184 proposed the following evolution of the friction coefficient:
with and the molar volume of X. Eq. is not thought to be general for non-solvent or not plasticizing molecules such as hindered phenols or aromatic amines. The fundamental reason is that such migrants are crystalline (solids) at high concentration.
It is worth noticing that can contain additional concentration dependence due to the extra free-volumes brought by the solute itself and the possible shift in the glass transition temperature. For most applications and in the absence of a unified theory, the equation of Fujita can be applied to describe the concentration dependence:
with a concentration to be determined experimentally.
5.2 Effect of the geometry of migrants on values
Migrants from polymer are not gas molecules, such as water, dioxygen, carbon dioxide, but heavy molecules larger than voids in the polymer. The smallest additives are monomer residues and solvents commensurable to one or several monomers. At the concentration of use of most of additives and residues (i.e., except plasticizers which obey to mutual diffusion), the many pair contacts between the segments of the polymer and the migrant control the rate of the translation of the most mobile species (the migrant). This configuration is very different from the situation in the food or in liquid food simulants, where the food constituents (water, oil, ethanol, etc.) are much smaller than polymer chains and are usually packed less densely. The correct picture is to consider that the trace diffusion of the migrant in the polymer is smaller than the self-diffusion of food constituents (typically 10-9-10-10 m2⋅s-1), but much larger than the self-diffusion of the polymer itself (<10-22 m2⋅s-1).
The exact mechanism of translation of molecules larger than voids in solid polymers has not been fully elucidated yet. They have been investigated independently by two communities: the community of free-volume-theory was interested in the mutual-diffusion of polymer solvents whereas the food packaging community was focused on the development of practical overestimate models for compliance testing. Due to the different nature of the considered substances and the type of considered diffusion coefficients (mutual diffusion measured in 1H spin-echo nuclear magnetic resonance and trace diffusion coefficients measured via desorption kinetics), the interactions between the two communities have been limited. Based on the work 136, 185, a unified approach has been sketched and is summarized in Figure 17. Early works 138, 186-189 suggested that the volume of the entire molecule or its rough estimate the molecular mass (see the discussion in Ref.190) offered a proper scaling parameter of diffusivities, at least, at the first tier. The use of the entire mass or volume of the migrant is misleading as it covers very different realities for rigid and flexible solutes. Flexible migrants, possibly with large masses, can benefit from the translation of smaller rigid units; whereas a large rigid migrant rarely requires free-volumes matching the shape and size of a larger rigid block. Without paying attention, both the effects of block sizes and their numbers combine, giving an apparent correlation of the logarithm of with the logarithm of the molecular mass (concerted displacements of rigid units or blocks) and with the total volume of the migrant . In this description, short n-alkanes are partly rigid since the constraints of torsion prevent blocks from translating independently.
Figure 17. Scaling of Diffusion coefficients between rigid and connected blocks with molar mass and Van der Waals volume in a thermoplastic polymer (groups A and B refer to substances defined in Figure 18).
Figure 18 reports the diffusion coefficients of 49 substances (105 values) in low-density polyethylene (LDPE) at 23°C collected by the National Institute of Standards (NIST)191 and the European Commission (EC) 192 from literature. The data were selected to reproduce the main features of Figure 17: the decrease of values with the number of rigid blocks and the almost invariance of with the exact shape and flexibility of the solute. The concept of invariance considers here that there is no visible effect if the induced variation is lower than the uncertainty associated with the measurement of . As an illustration of Ref.138 showed that the group of substances denoted A and B presented differences in diffusivities, which could not be explained by the differences between molecules. Three parameters were considered: the van-der-Walls volume ( in Å3), the gyration radius and the shape factor. Linear alkanes scaled as a power law with the molecular mass , with of 1.58 (range: 1.09-1.68) for [1] NIST data and 1.84 (range: 0.75-2.01) for [2] EC data. For bulky solutes, the large uncertainty in the experimental values suggests that diffusivities can be considered significantly different only if the differences between molecules are larger than 35 3. The correlation with volume is consistent with the free-volume theory of diffusion 136, and as is also correlated with the number of heavy atoms (see Figure 18e, the correlation depends on the type of substances), a reasonable upper envelope of values has been proposed to overestimate diffusivities185. The equation is coined Equation of Piringer:
with the key parameters and for LDPE. The values for other polymers are reported in the EU report 143. The model of Piringer provides only a variable overestimation ranging from a factor 0.63 (underestimation) to 100 (see the inset Figure 18a).
Figure 18. Scaling of diffusion coefficients of 49 substances (n-alkanes, two groups of molecules A and B with similar values) in LDPE at 23°C with molar mass, M, and the van-der-Walls volume. Data from: [1] Ref.193, [2] Ref.191, 192.
1: methane [1]; 2: ethane [1]; 3: propane [1]; 4: n-pentane [1,2]; 5: n-hexane [1,2]; 6: n-heptane [1,2]; 7: n-octane [1,2]; 8: n-decane [1,2,A]; 9: n-octadecane [1]; 10: n-dodecane [2,A]; 11: 2-trans-3,7-dimethyl-2,6-octadien-8-ole (geraniol) [A]; 12: 3,7-dimethyl-6-octen-1-ol (citronellol) [A]; 13: n-decylaldehyde or n-decanal (aldehyd c10) [A]; 14: 3,7-dimethyl-1-octanol [A]; 15: decylalcohol or 1-decanol [A]; 16: cis-undecen-8-al (aldehyd c11 inter) [A]; 17: n-undecen-2-al (aldehyd c11) (2-undecenal) [A]; 18: n-undecylaldehyde (aldehyde c11) [A]; 19: ethyloctanoate [A]; 20: 2-methoxy-4-propenylanisol (methylisoeugenol) [A]; 21: citronellyl formate or 6-octen-1-ol, 3,7-dimethyl-, formate [A]; 22: 2-methyl-3-(4-isopropyl)phenylpropanal (cyclamen aldehyde) [A]; 23: 2,6-octadien-1-ol, 3,7-dimethyl-, acetate, (2e)- (geranyl acetate) [A]; 24: 3,7-dimethyl-1,6-octadien-3-ylacetate (linalylacetate) [A]; 25: allyl-3-cyclohexylpropionate [A]; 26: amylcinnamicaldehyde or 2-phenylmethylene-heptanal [A]; 27: 3-methyl-3-phenylglycidate (aldehyde c16) [A]; 28: iso-amylsalicilate [A]; 29: benzylbenzoate [A]; 30: diethylphthalate (dep) [A]; 31: 2-hydroxy-4-methoxybenzophenone (chimassorb 90) [A]; 32: 2-methyl-undecanal (aldehyde c12 mna) [B]; 33: 3,7-dimethyl-6-octen-1-ylacetate [B]; 34: 3-[4-tert,-buthylphenyl]-2-methylpropanale (lilial) [B]; 35: 2,4-di-t-butylphenol [B]; 36: 2,6-di-t-butylphenol [B]; 37: 4-(2,6,6-trimethyl-2-cyclohexen-1-yle)-3-methyl-3-buten-2-one (methylionone-gamma) [B]; 38: 5-(2,6,6-trimethyl-2-cyclohexen-1-yle)-3-methyl-3-buten-2-one (methylionone-alpha) [B]; 39: 4-[4-methyl-4-hydroxyamyl]-3-cyclohexen-carboxaldehyde (lyral) [B]; 40: 2-hexyl-3-phenyl-2-propenal [B]; 41: 2,5-tertbutyl-4-hydroxy-toluene [B]; 42: 2,6-di-tert-butyl-4-methylphenol [B]; 43: 2,6-di-tert-butyl-4-methylphenol (ionol or BHT) [B]; 44: phenylethylphenylacetate [B]; 45: nonane-1,3-dioldiacetate (jasmelia) [B]; 46: 2-hydroxy-4-ethanediolbenzophenone [B]; 47: 2,6-dinitro-1-methyl-3-methoxy-4-tert,-butylbenzole (moschus ambrette) [B]; 48: 2-hydroxy-4-butoxybenzophenone [B]; 49: 2,4,6-trinitro-1,3-dimethyl-5-tert,-butylbenzene (moschus xylol) [B]
5.3 Effect of the polymer;
The effects of the polymer on the diffusion of migrants are twofold: i) the relaxation of polymer segments affect the renewal of free-volumes around the solute and ii) specific interactions between rigid blocks and the polymer may increase the release time of rigid blocks. In the original free-volume theory of Vrentras and Duda 133, 134, the translation of rigid blocks is assumed to be associated with the local reorganization of special free-volumes, so-called hole free-volume (hFV), whose redistribution is not activated by temperature. As an approximation of the thermal expansion of polymers, the amount of hFV available for the diffusion of migrants is proportional to , where is the glass transition temperature and a constant possibly dependent on the polymer and the shape of the translating block. This interpretation is illustrated on the diffusion of various migrants in rubber ( ) and glassy ( ) polymers in Figure 19. The apparent scaling exponent decreases rapidly with ; for linear solutes, Fang et al.185 demonstrated that its general expression was:
with essential a polymer-dependent constant and a positive constant for rigid blocks smaller than the cross-section of polymer segments and negative otherwise.
Eq. XXX and Figure 19a demonstrate that mass dependence increase rapidly when approaches or goes below . In elastomers and rubbers (with very low ) as well as in polymer melts, the mass dependence for linear migrants approaches unity. This theoretical value corresponds to the independent displacements of jumping units. Due to the dependence of with the type of rigid blocks, Eq. describes different mass dependence (see the three series of linear molecules in Figure 17) for different molecules. Although approximative, the technique can be used to extrapolate the results of from one polymer to a new polymer (denoted R) via the correction . The principles are illustrated in Figure 19e by showing that almost any of the presented polymer (except rubbers) can be used to predict the diffusion coefficients of the same substances in polypropylene only by setting the of the source and destination polymer. The same correction can be used to predict diffusivities in plasticized polymers from their values in non-plasticized ones.
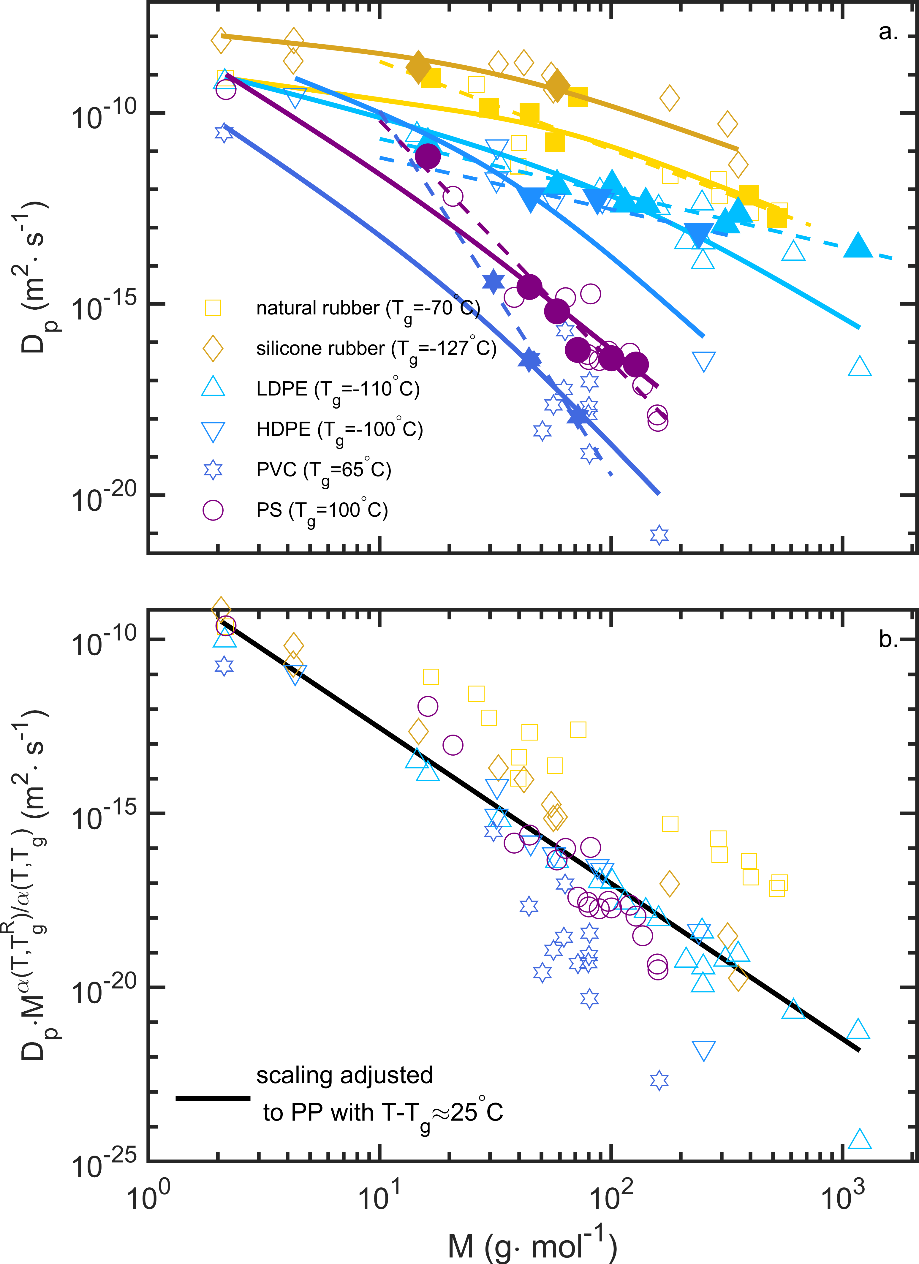
Figure 19. Diffusivities of various substances at 25°C in glassy and rubber polymers: (a) raw values, (b) normalized data to remove polymer effects (standardized to value of 0°C corresponding to atactic polypropylene PP). Filled symbols correspond to n-alkanes (scaling laws as dashed lines) and empty symbols to various solutes included gases and plastic additives (scaling laws as continuous lines). Data from Ref. 81.
5.4 Activation of diffusion by temperature
Increasing temperature affects firstly the structure of the polymer, which, in return, facilitates the translation of the migrants. Temperature activation is consequently higher in polymers with high thermal expansion coefficients (higher at rubber state than at glassy state, higher in plasticized polymer than in non-plasticized one, higher in thermoplastics than in thermosets). Below or near , apparent activation energies are dominated by free-volume effects and are higher than at higher temperatures. The effects of temperature for linear solutes near are shown in Figure 20. If the behavior was strictly Arrhenian, the dependence of would be linear with , which is not obviously the case for large diffusants near . Apparent activation energies increase with the size of diffusants as . The interested reader will find a consistent review of free-volume and specific-migrant activation in Ref. 136. In any case, it is not recommended to extrapolate values from low temperatures to high temperatures for polymer recycling, as it would overestimate diffusivities and consequently the rate of decontamination of the polymer.
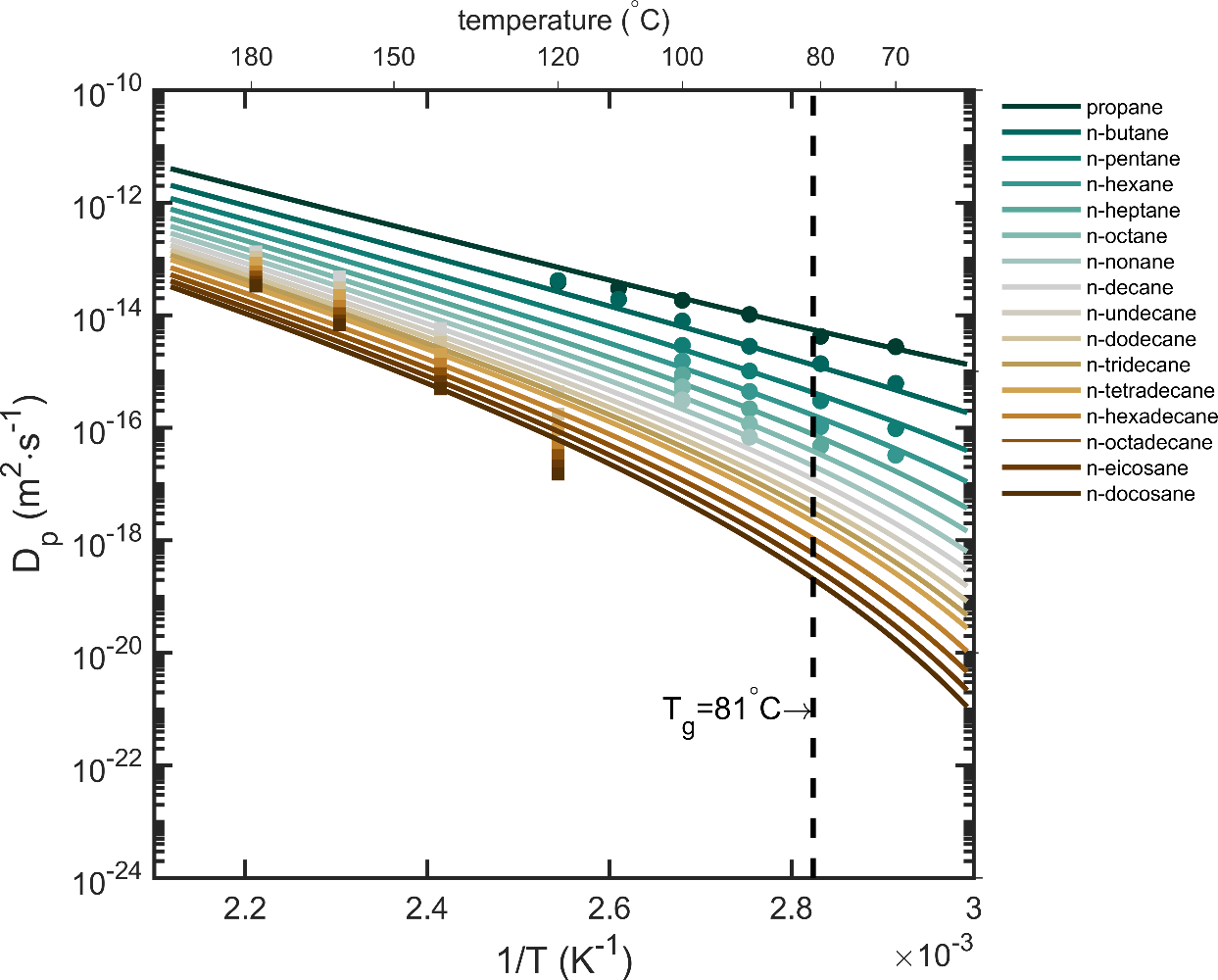
Figure 20. Arrhenius plot of diffusivities of n-alkanes in polyethylene terephthalate. Data from Refs. 188, 189, 194.
6 Sorption properties and partition coefficients
Highlights on the sorption and partition properties
- Along diffusivities, sorption and partitions coefficients are essential properties to assess the kinetics of migration in food.
- Along with fugacities, partial pressures offer the best representation of the force enabling a substance to move from one phase to the other. Practical approximations are given for all practical cases of mass transfer (from a material to a liquid, from a material to a gas phase, etc.) and possible substances (volatile or not).
- Partition coefficients are defined respectively to activity coefficients.
- Binary and ternary Flory isotherms offer estimations of activity coefficients for all applications of migration modeling: mixture of food simulants, wet or plasticized polymers, homo, and copolymers
- Temperature effects are less important between two condensed phases, but dominant between a condensed and a gas phase.
- Activity coefficients and they activation by temperature can be calculated at atomistic scale for arbitrary solutes (non-charged)
As shown in §4.2.1.1 and §5.1.2, sorption properties and partitioning between materials, food and polymer affect both the kinetics of migration and the distribution of migrants at thermodynamical equilibrium. Previous descriptions were essentially counting the number of substances in a representative elementary volume or a compartment (material, food). The present description will explicit the role of pair interactions between the migrant indexed and all other constituents ( for the polymer, for the contact phase, for ethanol, for water). Generic phases in equilibrium (in contact or not) are denoted , and regardless they are a solid (polymer or solid food), a liquid contact phase or a gas (headspace, storage environment).
6.1 Some definitions
6.1.1 Chemical potentials, fugacities, and activities
Two phases, and , are said at thermodynamical equilibrium if they are at the same temperature , pressure and the same chemical potential for any migrant : . The concept of thermodynamical potential was proposed by G. N. Lewis, with initially in mind pure ideal gases verifying , with is the molar volume of the gas . After integration at a constant temperature, the change in chemical potential from pressure to is for pure ideal gas. Lewis generalized to phase mixtures (ideal or not) by replacing pressure by a function , called fugacity and assessing the capacity of a substance literally to flee:
Reference values at the temperature and are physically related, but the choice of the reference chemical potential or the reference fugacity is arbitrary. The ratio defines the activity of the solute in the phase ; it provides namely a measure of the difference of the substance(s chemical potential in with its reference state. To describe mass transfer between the phases and (i.e., with ) at equilibrium is convenient to choose the same reference state in both phases. Following the intuition of Lewis, equivalent partial pressures in an ideal gas offer an almost universal potential to estimate the potential of transfer of any substance (e.g., a volatile organic compound, a liquid plasticizer, a crystalline pigment or a poorly soluble additive or mineral oil residues). The reference fugacity needs to be adapted accordingly as shown in Table 7.
Table 7. Expressions of practical partial pressures and saturation concentrations in relationship with the reference state of the substance in the conditions where its migration its studied.
| Application | Choice for the fugacity: | Choice for the reference fugacity: | Relationship with the concentration of substance in the phase : (SI unit in mol⋅m-3) |
|---|---|---|---|
| Volatile substance in a gas phase (=gas phase) | partial pressure: | total pressure: P | |
| Dissolved substance in a condensed phase (polymer, liquid) with a liquid reference state (=P or F) | partial pressure (equivalent partial pressure in the theoretical gas phase in equilibrium with ): | saturation pressure of the pure substance at the same temperature: | with the activity coefficient of the substance in the phase relatively to its volume fraction . At saturation, one gets: |
| As above but with a solid reference state | partial pressure (equivalent partial pressure in the theoretical gas phase in equilibrium with ): | Partial pressure at the surface of the crystal expressed as: with being the ratios of fugacities of the pure solute between solid (pure crystalline) and molten (pure amorphous) state. |
Migrants with a reference solid state in the conditions of migration are very common in plastics and thermosets. They encompass almost all antioxidants, colorants and pigments. They are liquid in conditions of processing of the polymer (e.g., above 160°C), but solid in the conditions of service of the finished material (at and ). The partial pressures are lower in this case but non-zero. The variation of fugacities between a pure crystal and its pure amorphous state depends on the temperature difference between and its melting temperature, as shown in Figure 21.
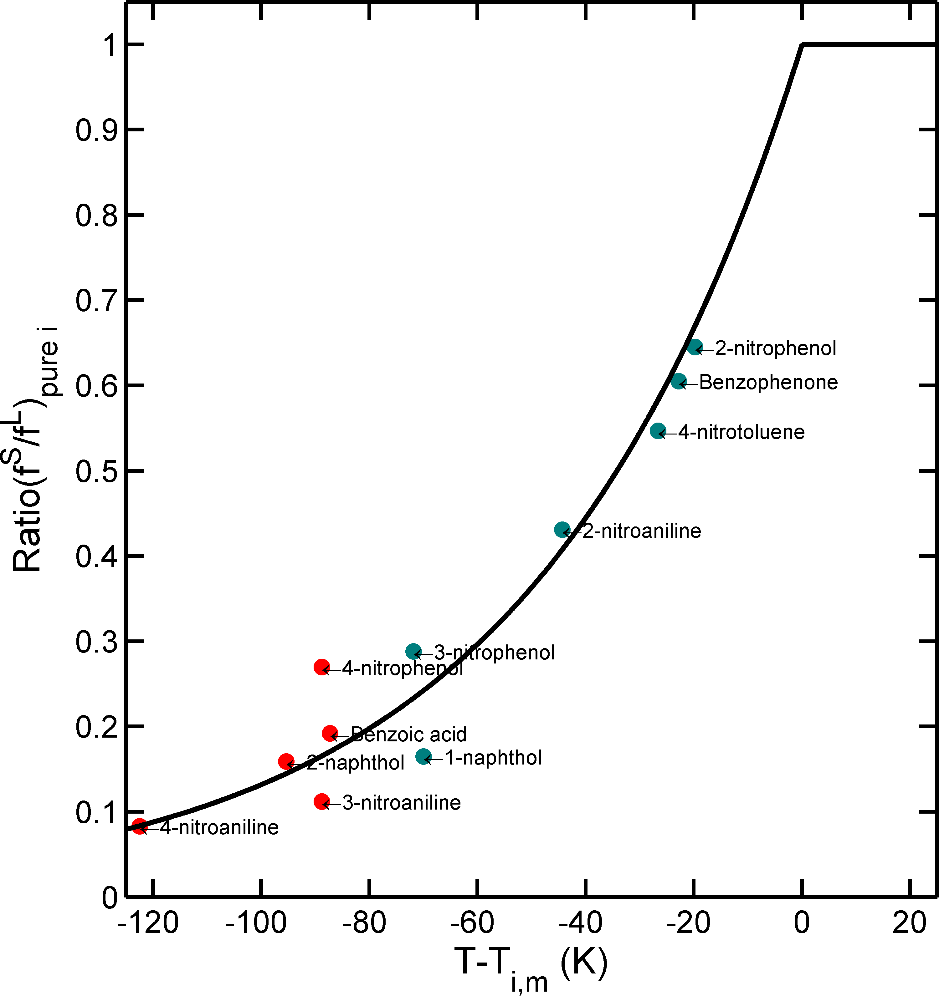
Figure 21. Ratio of fugacities between pure solid and amorphous states for 11 model migrants (data from Ref. 31) and its continuous approximation proposed in Figure S1 of the Supporting Information of Ref. 160.
It is worth noticing that thermodynamical models and simulations calculations may use different reference states (e.g., amorphous reference states even if the reference one is solid). The choices presented here are consistent with the definition of the molar solvation energy:
with being the effective partition coefficient between the condensed phase and the theoretical ideal gas phase . Respectively to mass transfer, the use of partition coefficients should be preferred to solvation energies. Free energies need to be preferred to analyze and to interpret quantitatively the nature of the interactions (van-der-Waals, electrostatic, hydrogen bonding) in the phase . Thermodynamic integration at molecular scale offers direct access to without requiring a theoretical separation of enthalpic and entropic effects.
6.1.2 Effective partition coefficients between P and F
From relationships presented in Table 7, effective partition coefficients between a material P and the contacting phase is given by the ratio of activity coefficients. For semi-crystalline polymers, it is well accepted that crystallites and crystalline phases are impenetrable to migrants. By assuming that no migrating substance has been trapped during processing in the crystalline phase, the effective partition coefficient reads:
where refers to the volume fraction in the amorphous phase of the material (possibly porous and semi-crystalline); and are the volume crystallinity and porosity of the material. Thermoplastics are not porous materials and .
For very porous materials, such as papers, it is preferable not to homogenize concentration between all phases (solid crystalline, solid amorphous and gas) and to choose the fibers as P and to adapt the exchange surface area to the shape of fibers. The characteristic dimension of the material should be chosen accordingly commensurable to the half-diameter of fibers.
6.2 Sorption isotherms
Sorption isotherms are experimental or theoretical curves, which relate the amounts absorbed by a condensed phase in relationship with an applied activity at constant temperature and pressure. Their use is more general than partition coefficients, when the values of depend on concentrations. In this section, we call isotherm a curve relating the activity coefficient or the excess chemical potential (i.e., in excess respectively to the ideal contribution ) with the composition in the mixture.
6.2.1 Linear isotherms
For most applications at infinite dilution, activity coefficients can be assumed independent on composition. The relationship between mass uptake and partial pressure is linear and governed by a Henry isotherm (see Eq. XX). The relationship between the Henry constant and is given by:
It is worth noticing that if the condition of infinite dilution is well verified in foods regardless the considered substance (migrations are expected to be low), it may not be verified in the material for substances used close to the saturation (e.g., pigments) and for plasticizing substances (e.g. used at weight fractions up to 50%). The proposed description assumes that the substances are well mixed and exclude, by definition, surfactants, and substances causing blooming.
6.2.2 Binary Flory isotherms
General formulation
Flory-Huggins theory offers a robust framework to account for concentration effects. The theory extends the regular solution theory for liquid mixtures to mixtures with molecules with dissimilar sizes such as solutes mixed with polymers segments or large additives dispersed in a food simulant. Enthalpic and entropic interactions are calculated on a lattice assuming that the mixture is incompressible and that molecules fill space commensurably to their molar volumes. For binary mixtures, or , the activity coefficient is given by:
where is the size of the host molecule respectively to the size of the solute . In a polymer, the chain is considered infinitely long . In foods and a liquid simulating the food, represents the number of molecules of F displaced by the insertion of the substance in F. For most of the migrants, is expected to be larger than unity in water and ethanol and lower than unity in oil. can be approximated as with [n_{k\ around\ i}^{compressible}] accounting for the partial compressibility of the molecules of and. Rigorously, partial molar volumes should be used instead of molar volumes.
Approximation at infinite dilution
At infinite dilution and pending estimations of the Flory-Huggins coefficients , Eq. provides an estimator of activity and partition coefficients in amorphous regions:
Effect of temperature on partitioning
According to Eq. , the variation of with temperature depends on the variation of the difference with . When and are of the same sign, their variations with are similar and compensate each other. When , there is no compensation and the effect of temperature is maximum (case of polar solute distributed between a polar and an apolar phase). In both cases, the absolute values of tend to decrease with temperature, so each mixture becomes progressively ideal (i.e., with no enthalpy of mixing). The temperature dependence is predicted via Eqs. -.
6.2.3 Ternary Flory isotherms
Eq. can be generalized to ternary mixtures with two practical applications: i) the estimation of activity coefficients in polar polymers, which contain some amount of water, and ii) the estimation of activity coefficients in water-ethanol mixtures.
The activity coefficient in a wet polymer, associated with a volume fraction of water , depends on the three pair of Flory-Huggins coefficients, , (water in dry P), (solute in water), as (see Eq. 9a in Ref. 31):
The activity coefficient in water-ethanol mixtures or in any mixture of two miscible liquids F1 and F2 can be estimated similarly 158:
with being a ternary Flory-Huggins coefficient, whose contribution can be neglected in the absence of specific ternary complex in the solution. The binary Flory-Huggins coefficient between water (F1) and ethanol (F2) is obtained from the molar heat of mixing of the mixture, , as . Using the polynomial approximation proposed for water-ethanol mixtures in Ref. 195. Figure 22 reports the value of with the volume fraction in ethanol as well as the values for common food simulants expressed in alcohol-by-volume (abv) instead of volume fraction. The volume fractions ethanol and water in the mixture are tabulated from their partial molar volumes between 10°C and 60°C in Table 8.
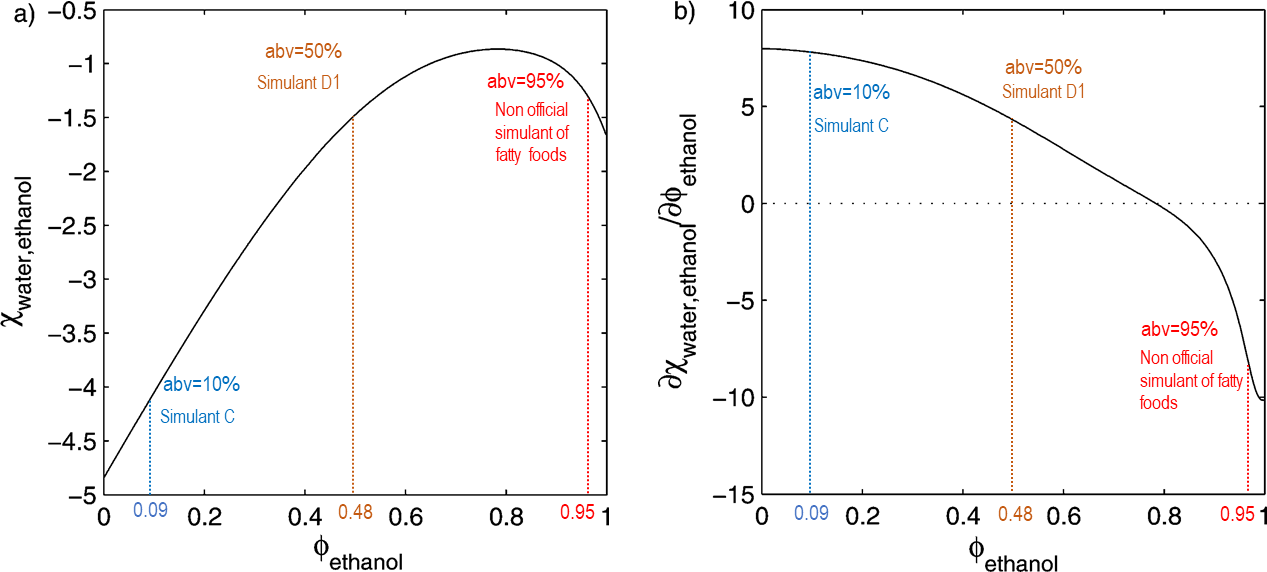
Figure 22. Variation of the binary Flory-Huggins coefficient in water-ethanol mixtures. Data from Ref. 158. “abv” values represent the equivalent alcohol strength (alcohol-by-volume at 20°C and atmospheric pressure). Simulant C: 10% ethanol for alcoholic foodstuffs; simulant D1: 50% ethanol for high alcoholic and milk.
Table 8. Density (kg⋅m-3) of water-ethanol mixture and corresponding volume fraction of ethanol () between 10 and 60°C. Volume fractions are calculated from partial molar volumes. =alcohol-by-volume at 20°C.
| 10°C | 10°C | 20°C | 20°C | 30°C | 30°C | 40°C | 40°C | 60°C | 60°C | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.0 % 7.0 % 10% 12 % 15 % 20 % 30 % 40 % 50 % 60 % 70 % 80 % 90 % 95 % 99 % | 992.6087 990.0815 986.5772 984.3969 981.3355 976.6829 967.1218 954.5007 937.5325 917.0055 893.7478 867.6778 837.7669 819.9502 802.7596 | 0.0463 0.0640 0.0903 0.1080 0.1339 0.1773 0.2695 0.3722 0.4773 0.5812 0.6847 0.7889 0.8940 0.9478 0.9900 | 991.0594 988.4460 984.7554 982.3832 978.9701 973.5916 962.2368 948.0405 930.1519 909.1314 885.5598 859.2628 829.2000 811.3845 794.2436 | 0.0465 0.0643 0.0912 0.1092 0.1356 0.1800 0.2739 0.3755 0.4795 0.5828 0.6858 0.7896 0.8946 0.9479 0.9900 | 988.4199 985.7365 981.8636 979.3060 975.5866 969.5825 956.6964 941.2003 922.4957 901.0173 877.1417 850.6228 820.4500 802.6589 785.6217 | 0.0466 0.0646 0.0920 0.1103 0.1372 0.1826 0.2775 0.3789 0.4816 0.5844 0.6869 0.7906 0.8950 0.9481 0.9901 | 984.8805 982.1110 978.0521 975.3416 971.3450 964.7720 950.5944 933.9794 914.5695 892.6443 868.4696 841.7478 811.4700 793.7375 776.8538 | 0.0467 0.0650 0.0928 0.1113 0.1386 0.1847 0.2807 0.3816 0.4837 0.5859 0.6883 0.7915 0.8954 0.9482 0.9901 | 975.3125 972.3164 967.9100 965.0044 960.6287 953.2020 937.1834 918.9400 898.2414 875.3261 850.5234 823.5828 792.9257 774.9002 758.1182 | 0.0473 0.0660 0.0938 0.1125 0.1407 0.1883 0.2857 0.3863 0.4877 0.5894 0.6908 0.7929 0.8971 0.9491 0.9900 |
6.2.4 Binary Flory-Huggins coefficients in a copolymer AB
Based on calculations at molecular scale, Nguyen et al. 160 demonstrated that Eq. (12) in Ref. 31 was acceptable for copolymers consisting of repeated blocks shorter than the persistence length of polymer segments. The corresponding Flory-Huggins interaction coefficient in a copolymer AB, , reads:
Eq. XXX is based on an averaging of all possible contacts between and , where the term represents the additional cohesion energy brought by the interactions between A and B. It can be generalized to more complex copolymers while the contacts can be assumed perfectly random (i.e., no macro or microphase separation).
6.3 High throughput calculations of Flory-Huggins coefficients at atomistic scale
6.3.1 Justification and limitations
Molecular modeling offers a good alternative to time-consuming and complex experiments to estimate Flory-Huggins coefficients for various substances: monomers, oligomers, solvent, additives, residues, breakdown products, non-intentionally added substances. The results can be tabulated in advance and used directly with Eqs. - for a broad range of applications. With this respect, they are more intrinsic than partition coefficients. In details, molecular modeling can be seen as an alternative to earlier group contribution methods relying on estimating Flory-Huggins coefficients from solubility parameters (see Ref. 110, 149). The limits of the approach have been discussed in Ref. 112 and compared with calculations at atomistic scale. In shorts, group contribution methods provide only an average picture of the interactions. The real conformation of molecules and the distance between interacting chemical groups are, in particular, not preserved. The principles of calculation of and have been reviewed in Refs.112, 158-161. They apply to any homo and copolymer as well as almost to any solute while no net charge is present on the polymer, on the food simulant or the solute. The main limitations are intrinsic to the Flory approximation itself: no energetic barrier should exist in the host system (P and F) so that all states are accessible. It is not true in glassy polymers, where hysteresis is frequent. The contribution of the subcooling and accumulated elastic energy can be introduced a posteriori by combining Flory and free-volume theories together148, 196. These extensions are, nevertheless, beyond the scope of the chapter.
6.3.2 Principles
The Flory-Higgins coefficients, is defined as the dimensionless mixing energy (enthalpy) in excess relatively to pure compounds:
where represents an ensemble-average of , is the length used in the approximation of the polymer and . In agreement with the original Flory approximation, enthalpies are estimated by summing energies of contactwhen B is contacting the seed molecule A. represents the same energy when B is used as seed molecule. In practice, is calculated by choosing an orientation randomly for the contact molecule and by translating it along a random line until at least one point of contact is established between the van-der-Walls surfaces of the contact and seed molecules. The process is repeated for all conformers and stereoisomers considered. Finally, is estimated as the product of contact energies and the number of neighbors (number of B molecules surrounding A):
Eq. XXX assumes that and statically independent (zero covariance). For polymers, the property of independence is achieved from a sufficiently large value so that the surface of contact of the polymer is independent of the length of the considered polymer. The main advantage of the whole approach is that there is no need to represent entanglements in the polymer and free-volume. The shape of the backbone of an infinitely long chain with shorter oligomers by preventing head and tail atoms from coming in contact with any van-der-Wall surface. Cooperative hydrogen bonding is accounted by using a value of greater than one. The latent heat of vaporization of water can be correctly approximated by using a value of different to unity. This value depends on the type of forcefield used to simulate water. As an example, the rigid water model governed by the TIP4P forcefield gives an acceptable value with whereas is required with same forcefield but using to three-point charges (forcefield TIP3P). The number 4 enforces in this case that any water molecule is on average involved in 4 hydrogen bonds of similar strength.
Contact energies are calculated irrespectively to any temperature consideration. The effect of temperature is recovered by weighting the distribution of contact energies with the Boltzmann factor :
At the price of calculating two integrals, Eq. can be used to estimate at several temperatures. Conformers need to be generated in a way they are representative of their conformations (radial distribution, constraints of torsion) in the corresponding condensed phase. In practice, they are sampled from molecular dynamics simulations of the equivalent condensed phase.
7 Probabilistic modeling of the migration
Highlights on probabilistic modeling of the migration
- Conventional modeling calculates point estimates, associated to the most likely combination of inputs. Probabilistic modeling calculates the statistic distribution of the amount transferred for all combination of the parameters (likely or not).
- Theoretical results make the calculations of sensitivities and statistic distributions almost as fast as point estimates.
- The combined effects of uncertainty and variability (e.g. residence times at specific temperatures) can be analyzed together and used to provide conservative estimates with controlled a risk of underestimation.
- The same approach can identify the most influential parameters acting on the value of the migration or the final decision value.
7.1 Beyond intuition
Any risk assessment procedure needs to account the possible variabilities in the considered scenario (e.g. variable temperature, contact time) and the numerous sources of uncertainties inherent to the limitations of our knowledge and oversimplifications. Variability and uncertainty can be easily recognized and separated by noticing that only uncertainty can be reduced by bringing additional knowledge or refinement. By contrast, variability represents multiple values of several instances (lots, compositions, final use), storage conditions, etc. For compliance testing, conservative assumptions are mandatory, but the relationship between the maximization of parameters (or their minimization depending on the case) and the maximization of the amount transferred is straightforward only in simple configurations: one material or one single layer, one step, no variable conditions.
The intuitive approach for is illustrated in Figure 8 for a single component and monolayer packaging in contact with food. When the whole food-packaging system is perfectly impervious (no loss to the outside), the cumulated amount leaving the packaging-food interface is a monotonic function of the time, the initial concentration, the diffusion coefficient in the polymer, the chemical affinity for food, the temperature, etc. As a result, choosing a conservative or upper bound for all inputs guarantees an overestimation of the food contamination. In the presence of multiple materials or steps, the property of monotonicity between parameters and inputs is not mathematically verified anymore. In particular, food contamination can be maximum before reaching equilibrium. For example, overestimating all diffusion coefficients or partition coefficients in laminates will spread migrants everywhere instead of bringing them faster to the contacting phase. For laminates, methods described in §4.2.3.5 and theorized in 98 can be used to recover conservative estimates. The calculation procedure consists in splitting the contribution of components/materials into independent simulations and in cumulating the concentration in food: . The algorithm is sketched for a substance present simultaneously in the walls (bilayer AB, B is contact) and the cap of the bottle (C). The problem comprises materials and requires simulations:
- One-dimension mass transfer simulation from B to the food (without A and C) to calculate
- One-dimension mass transfer simulation from C to food (without A and B, i.e. no walls).
It is worthwhile noticing that the scenario described is also conservative if we assume that the substance has been distributed between A and B before being put in contact with the food. It also covers the case when is initially located in A and not in B (see Figure 10), but with a higher safety margin.
7.2 Epistemic uncertainty
In system engineering, reliability and safety are quantified with respect to some safety margins, defined as the differences between reference values accepted by the regulating body and calculated values. A system is considered safe when the differences calculated for a set of postulated scenarios verifies a minimum distance or when the probability of the distance to be zero or negative is lower than some prescribed value. Introducing conservatism randomly by mixing worst-case bounds may propagate uncertainty fuzzily and leads to uncontrolled overestimation of the amount transferred to the food. At the beginning of the supply chain, the chemical industry and compounders face mainly variability on the different applications of their chemicals and raw materials. On the opposite side of the supply chain, the packaging filler and the retailers face a more different situation with strong uncertainties on the nature of the materials, their thicknesses, their composition. In 2009 and despite the possibilities offered by EU directive 2002/72/EC, we evaluated that migration modeling could be helpful to demonstrate the compliance in finished products only in less than 5% of cases 112. The chief reason was the loss of compositional information along the supply chain. Calculations could be done on part supplies and compounds to produce certificates of food contact compliance, but not on the full system assembled in the intended conditions of use of the packaging. Compositional information is currently better shared in EU and new deformulation techniques provide grounds for spreading calculation practices from the chemical industry to the food industry 114.

Figure 23. Illustration of safety margins (SM), overestimations factors (Q) and uncertainty according to the method of calculation: real, likely and very conservative.
The best practice for industry relies on sharing minimum information so that a significant safety margin remains for the end-user and keep the utility of migration modeling. As an illustration, Figure 23 compares the safety margins when over-conservative estimates and realistically overestimates are used. We attract the attention to the reader that the location of the “real” value is not known usually so that the overestimation factor cannot be guessed a priori. Only the safety margin is directly accessible to calculations. The definition of the safety margin and its usage in various technical guides and supporting risk assessment documents can be inconsistent and confusing. In particular, the concept of safety margin is frequently confused with the concept of overestimation. We used the definition of safety margin applied in medicine to evaluate drugs, in structural engineering, in nuclear engineering, The concept of overestimation applied to some factors including diffusion ( ) and partition () coefficients can be misleading. Indeed, their overestimation by a factor causes an overestimation of the concentration in the medium in contact which is not proportional. For the layer in contact, it varies from (short contact times) down to 0 (equilibrium) for diffusion (. For , it increases from 0 to a value, which depends on the volume of the food.
By evaluating uncertainty associated to realistic estimates, probabilistic modeling offers a robust methodology to assess the effects of the combined sources of uncertainties and finally to have no safety margin at all. The example depicted in shows that the upper limit of likely overestimates including uncertainty (95th percentile) offers a higher safety margin than the very conservative overestimate. The distinction between overestimations and realistic conservative estimates can be exemplified by considering a long contact at a variable temperature (e.g. due to transportation). A conservative estimate will calculate migration at the highest temperature, whereas a realistic conservative value will be provided by replacing time with its integral dimensionless version, Fourier number, . The proposed approximation does not introduce any significant approximation and can be carried out at the same cost as standard simulations (see §4.2.4 and Eq. XXX).
7.3 Sensitivity analysis of migration models
7.3.1 Local sensitivity analysis
Deterministic modeling and simulation yield the same output (concentration in food, concentration field in the packaging material) for the same set of inputs. The analysis of the sensitivity to input parameters entails evaluating the effect of a modification of each parameter (initial concentration, diffusion coefficient, partition coefficient…) on the safety margin, . Since the parameters have different units, it is convenient to calculate the derivatives of with respect to the logarithm of each parameter:
is the Jacobian matrix of the migration model and it can be used to evaluate a linear approximation of the safety margin when inputs are changed from to :
Eq. XXX provides analytical solutions only in simple configurations, but its application is very general. Additionally, implementing the difference as prevents the problem of step size known as subtractive cancellation. Its usage is shown for a variant of the realistic but conservative model for monolayer materials presented in 4.2.2 (see Eq. XXX):
The evolution of the safety margin reads when the input values are changed to from an initial set :
with .
Besides showing the interactions and additivity of the different sources of uncertainty, it offers a rapid methodology to identify the main influencing parameters without requiring any simulation or software. Eq. XXX also applies to numerical simulations, but it requires simulations (the reference one and variations). When the number of inputs increases, it is preferable to reduce the computational effort by using similitude principles and dimensionless numbers. In the detailed example, the use of a dimensionless time enables to test simultaneously the effects of , and . As Eq. is a first order approximation and, despite the use of a logarithm scale, it is losing accuracy as soon as parameters are tested beyond several factors.
7.3.2 Global sensitivity analysis via stochastic simulation
When the number of variables becomes large as well as the intervals to be explored, the statistical sampling of inputs is preferable. Statistical analysis of the outputs can be used to extract the influence of each variable and the probability to have the prescribed threshold exceeded. Each component of the vector needs to be sampled randomly and uniformly over its interval of interest. The technique is so-called Monte-Carlo trials and its numerical implementation stochastic simulation. By denoting samples chosen around the likely vector so that only the parameter is modified at a time, and by denoting the corresponding safety margins. The sample covariance is given by:
where is the average safety margin, which does not coincide with in the general case. represents the prediction associated with the 50th percentile.
Eq. XXX generalizes the local sensitivity analysis performed in Eq. XXX, based on small variations and partial derivatives. The concept of covariance enables to screen the whole input spectrum, to identify the interaction and dependency structure on all parameter including the analysis. If the geometry, the temperature and contact time are introduced, the design and the conditions of use can also be explored.
A probabilistic interpretation is achievable; but, as means and covariances provide only the first and second moments, a likely distribution of the safety-margin or the concentration in food is required. If the concentration in food is normally distributed, the problem is fully determined with the first and second moments. This assumption is valid only in the presence of a low range of variabilities and uncertainties. Indeed, the Gaussian distribution is unbounded, and it implies, even with very low probabilities, that the concentration in food could also be negative and the amount transferred could be higher than the amount in the material. The next section removes these limitations for risk assessment and the evaluation of consumer exposure.
7.4 Principles of the probabilistic interpretation of mass transfer
Global sensitivity analysis presented in 7.3.2 introduces the first interpretation of mass transfer with a marginal distribution on each input variable, which is assumed to be uniform. The combination of these variables and its interpretation is known as a copula in probability theory and statistics. Copulas describe well the dependence between inputs on the output(s) of a model, but they fail to describe the joint distribution of contamination in realistic situations. The diffusion and partition coefficients, as well as the initial concentration in food are not distributed uniformly. The industry is not applying randomly any concentration value or the molecules do not have random properties. It is our limited knowledge and the variability of practices that spread the inputs around a likely value. In shorts, the sensitivity analysis is a perfect tool to optimize the geometry, the formulation, etc. but it is not appropriated to get a reliable estimate of the probability to have a concentration threshold exceeded.
The principles of probabilistic modeling of migration have been described in 197 and applied to various cases 96, 97. The central idea is to combine a dimensionless formulation (with a reduced number of input variables) along with random numbers. For the same reason as invoked for the local decomposition in §7.1.3.1, each quantity is written as the product of a scaling value (with units), denoted (usually the likeliest value), and a random dimensionless number distributed around unity. As an illustration, the dimensionless time reads:
7.4.1 Input distributions
The distributions of can be chosen either from experimental measurements or from prior guesses or beliefs. In this second alternative, distributions which have a shape factor and non-negative, denoted , should be preferred (beta, Erlang, exponentially modified Gaussian, exponential, gamma, inverse-gamma, inverse-Gaussian, lognormal, Weibull…). For some quantities, such as concentrations or thicknesses, symmetric distributions are more realistic; truncated normal distributions can be used for this purpose. A non-exhaustive list of practical distributions is given in Table 9.
Table 9. Recommended distributions for probabilistic modeling of the migration from monolayer materials. The distributions of and are posterior distributions.
| random contribution | distribution | recommendations | ||
|---|---|---|---|---|
| rubber polymers | glassy polymers | |||
| diffusion coefficient | ||||
| contact time | † | to be determined | ||
| initial concentration | truncated† | |||
| thickness | to be determined | |||
| mass Biot number | ||||
| partition coefficient | ||||
| Fourier number | : to be calculated | |||
| concentration in food | : to be calculated |
† to be normalized to get a unitary expectation.
7.4.2 Estimation of probabilities via Monte-Carlo sampling
Probabilistic modeling aims at determining the cumulated density function (cdf), which can written for monolayer materials as the probability to get a value of lower than arbitrary number :
In the sake of efficiency, (see Eq. XXX) was used instead of . Indeed using Eq. , it can be shown that the distribution a posteriori of converges in law to a Gamma distribution with parameters . Ref 114 tabulates their values with , and .
The cumulated probability (or its complement ) can be estimated by repeating the simulations for different values of input parameters and by counting the number of occurrences, for which the inequality (or ) is verified. If the intent is to demonstrate that is low for a sufficiently large , we could think it suffices to apply some worst-case scenarios (bounds of intervals) and to demonstrate that the value is never exceeded. This approach is correct only if , that is for a value of larger than the one corresponding to a total extraction. In the general case, the intervals of all parameters need to be sampled with each value chosen according to its theoretical prescribed distribution. This technique of picking randomly input values and to launch the corresponding simulation is known as Monte-Carlo simulation.
In practice, for each input quantity , a random number is chosen uniformly between 0 and 1 (function rand() in many programming languages). The specific value to be included in the considered simulation vector will be , with being the cdf of the variable X. Depending of the size of the intervals, 103 to 105 simulations are required. For multilayer materials, the sampling effort can even higher. The total cost of simulations can be reduced dramatically by tabulating the results in advance for a significant range of dimensionless numbers and by subsequently interpolating the values of interest. These concepts are justified mathematically hereafter. They make the cost of probabilistic modeling close to the cost of deterministic modeling.
7.4.3 Estimation of joint probabilities via the composition theorem
The calculation of probability density functions (pdf) associated with a combination of variables (e.g., Eq. XX)X or with the resolution of partial differential equations is particular computationally expensive and requires a specific treatment of the joint density . The composition theorem offers a very efficient computational approach for invertible and differentiable transformations:
Mathematical functions represent either a variable transformation (e.g., Eq. ) or the full mass transfer model. The joint density of is given by the determinant of the Jacobian matrix , denoted :
Eq. XXX can be generalized to non-monotonic functions by splitting the transformation into intervals which are locally monotone. For example, in the special case where the dimensionless concentration in food is not a continuous function of (some multilayer or multicomponent configurations), the pdf of is obtained by the accumulation of the transformations over contiguous intervals:
with the partitions of where is piecewise monotonic.
7.4.2 Some illustrations
Probabilistic modeling must be envisioned as the generalization of deterministic modeling, but its clear definition depends how the normalization of is performed, how deterministic inputs are set (likeliest values or averaged ones) and how the transformation stretches or contracts the probability space. Deterministic modeling provides indeed the unique solution of the initial-value problem. Probabilistic modeling generates the distributions and the confidence tube including the solutions when the initial inputs are changed. The use of dimensionless number, such as a cumulated Fourier number including temperature variations or the ones associated to homologous solutes , offers even a broader interpretation by including random variations of temperatures or uncertainty on diffusion coefficients (see 138 for discussion). In the context of risk assessment, the scaling quantities , and as acceptable conservative estimates and the effects of uncontrolled variations and uncertainties can be captured with the distributions of , and or by choosing them equal to unity.
7.4.2.1 Typical probabilistic migration kinetics
Without loss of generality for estimating multivariate distributions of concentrations, the principles of composition are illustrated in Figure 24 for the dimensionless migration kinetics from monolayer materials (see. §). In this example, is the only random variable and all other parameters remain fixed (not distributed). The distribution of the dimensionless concentration is inferred from Eq XXX with (strictly monotonic curve). It can be viewed as the projection of the support of onto the curve . When the transformation is repeated for different values for , the upper and lower percentiles of the migration kinetics can be interpolated continuously with . Such curves are not accessible to the direct simulation and are not parallel to the deterministic or 50th percentile. The vertical distance between the extreme percentiles represent the resulting uncertainty in the amount transferred according to the original dispersion in values. It is worthwhile noticing that dispersion increases with time but that its effect on is decreasing after . Close to equilibrium, ceases to have a significant effect.
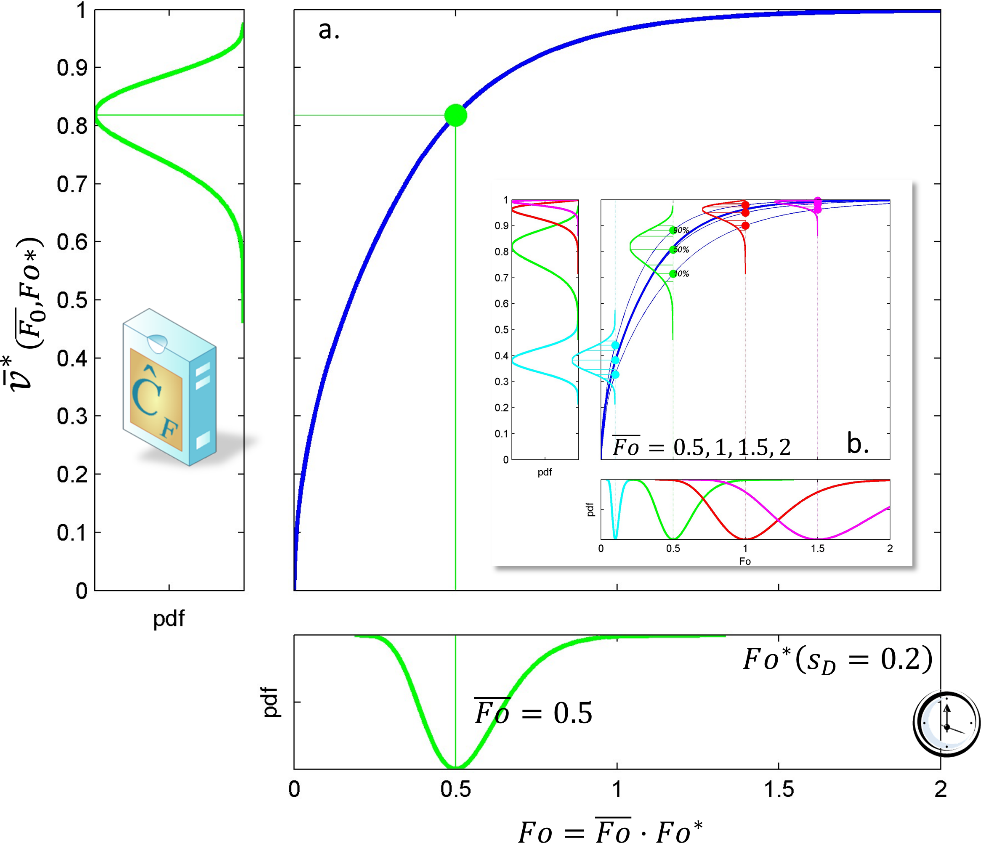
Figure 24. Probabilistic modeling of the contamination from a monolayer material via Eqs. and : (a) point distribution for ; (b) corresponding 10th and 90th percentile curves. The likeliest migration curve corresponding to the maximum probability (mode) of the Fo distribution appears in bold.
7.4.2.2 Effect of Bi and sD
The overall mass transfer resistance, , of any compartment (either the food or the packaging layer) is evaluated as or as , whether the chemical affinity of the substance is considered or not. For monolayer materials, the packaging-to-food mass transfer resistance ratio is given by and , respectively. values are expected to be large above 103 with well mixed and low viscous liquids in contact with thick or barrier polymers. Low values ranged between 5 and 103 were observed only in polyolefins in contact with liquids 198. In semi-solids, solids and dry foods in contact with polyolefins and plasticized polymers, migration kinetics linearizes with time 199 and approaches unity.
The effects of and are illustrated in Figure 25. Increasing the mass transfer resistance on food side (i.e., decreasing ) affects non-linearly the dispersion. As justified by Eq. XX and because the contamination is strictly increasing, the dispersion of the contamination is weighted by the term . As low values and large ones lead to low slopes of vs , the dispersion of concentration values are, as expected, maximum for intermediate concentration values far from the initial and equilibrium states. Increasing modifies strongly the shape of the median kinetics, the upper limits and of the overall distribution in food. The depicted example demonstrates that the migration can be overestimated reliably by considering a likely value for and by taking for example the 95th percentile of along with a proper value of . Doing the reverse, calculating from the 95th percentile of values does not guarantee that the value of the contamination is overestimated in 95% of cases. It is not verified in the case when the slope of changes rapidly with . This is true only when , as shown in Figure 25a.
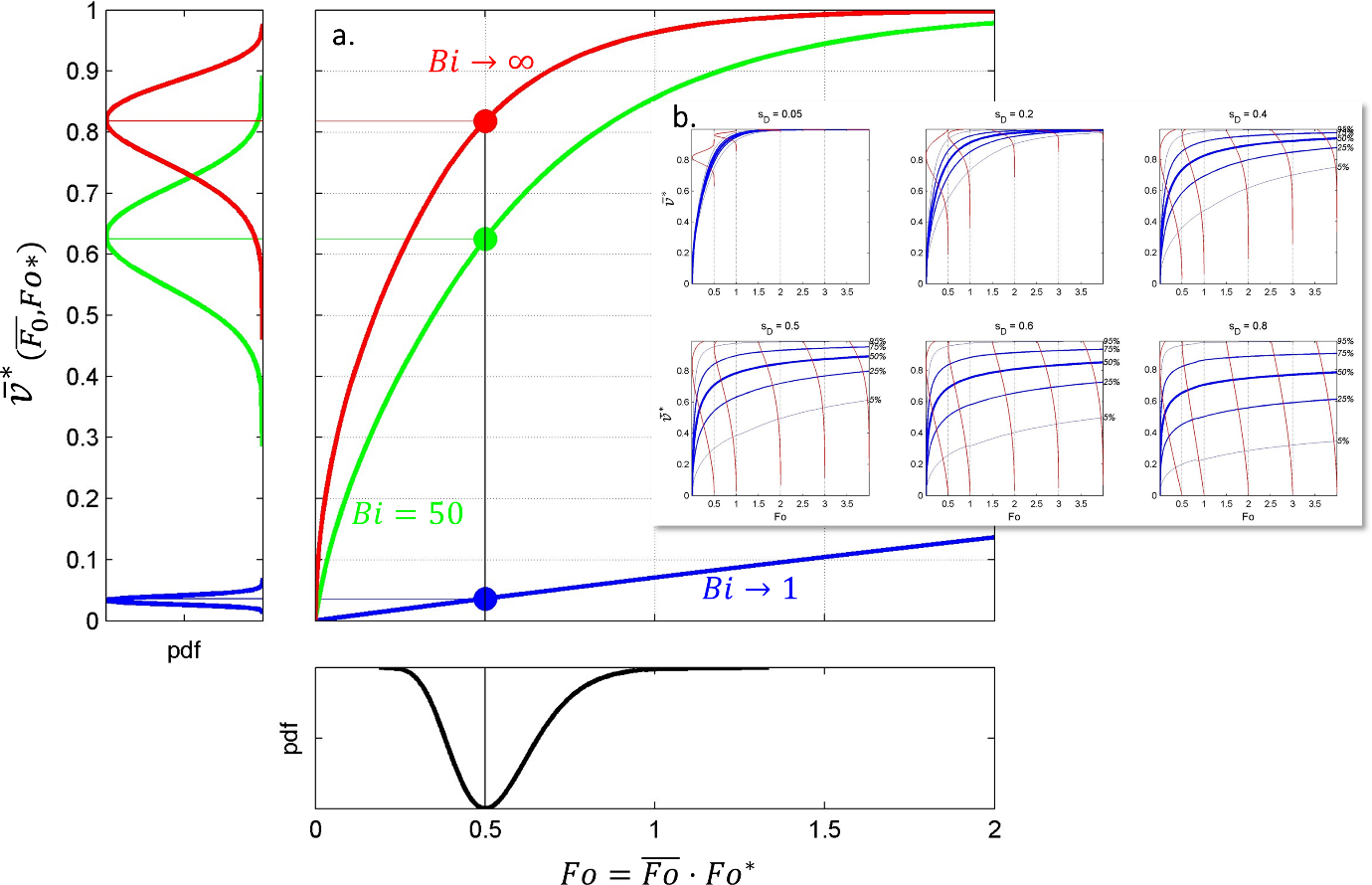
Figure 25. (a) Effect of on the dimensionless migration kinetics. (b) Effect of for (the percentiles are represented as equivalent kinetics; distributions of for =0.5, 1,2, 3 and 4.
8 What will be the future?
Highlights on new trends
- Because migration modeling is cost effective, its application spreads between countries and beyond its original application domain: food packaging in plastics.
- Migration modeling turn the fate of contamination into forecastable phenomena with causes and responsibilities.
- Migration modeling paves the way for a food safety managed in the cloud.
8.1 Extending the legal scope of migration modeling
A robust validation of the macroscopic equations of mass transfer (transport equations and boundary conditions) has been central to the development of the US legal system authorizing migration modeling in the years 90’. The European system focused during the two past decades on diffusion coefficients with much smaller attention on partition coefficients. In both cases, migration modeling is recognized and well accepted but only for thermoplastics. Its application to thermosets, elastomers, paper, and board is comparatively supported by a much small number of scientific and technical publications. Recently, Chinese regulation adopted migration modeling and equivalent calculations without material restriction. The move is a logical step after the substitution of negative lists by positive ones and the adoption of specific migration limits for a broad range of applications.
At the expense of proper significant safety margins, migration modeling has no limited scope and can cover multiple materials and complex conditions of use of food contact materials. The chief difficulty remains in practice the lack of information on the substances initially present in the materials and their amounts. Paradoxically, migration modeling offers an efficient and secure solution to the delicate problem of the declaration of conformity according to the position of the operator in the supply chain. At each step, the essential information to demonstrate the compliance and safety assessment respectively to intentionally added substances can be encoded into almost anonymous numbers (worst-case values of concentrations, properties, and thresholds), without revealing the exact details of formulations, chemical structures, etc. The amount of data could grow along the supply chain by adding new records (association of substances, materials, logistics data, date of production) and refined scenarios, which correspond to the final application of the packaging or the targeted market (e.g., country, food/pharmaceutical). In a very near future, the whole process could be included in a blockchain resisting to falsification and not requiring any third-party authority. Migration modeling software could process any node and verify rapidly hundreds of constraints corresponding to the integrity of all decisions. Date stamps and default expiration dates could alert in advance operators of the needs of revising either risk assessment or risk management decisions. All the effort related to typing inputs, looking into databases and estimating properties could be performed by scanning a QR code or equivalent. The result could be a new QR code verifiable by local authorities.
After several decades of pioneer developments and validation, the chemical industry, producers, converters, recyclers, food industry, retailers, authorities and consumer associations could turn into interoperable systems promoting both safety and economic efficiency. The definition of common standards (CEN, ISO) and training could be the first step. Respectively to modeling, the legal systems initiated for food contact materials and articles could also be used as templates for future evolutions of the regulation of materials used in cosmetic, pharmaceutical, medical, biotechnological, and clothing products.
The possibility of managing cross-contamination via modeling and simulation is expected to impact rapidly good manufacturing and handling practices. Migration modeling can be used, indeed, to establish the causality between practices and migration regardless their position in the supply chain and the distance between the incrimanted material and the food. Demonstrating causality will bring some form of responsibility irrespectively the material or the practice are intended to be in direct contact with food or not. As an example, the contribution of secondary packaging materials acting as large reservoirs of contaminants can be evaluated, as the foreseen effects of corrective actions, including air renewal in storage places, separation of printed and non-printed materials, separation of laminates from monolayer materials…
.
8.2 Extending the capacity of migration modeling
The validations of functional barriers and recycled materials have been the main successful applications of migration modeling. The last advance in migration modeling including multiscale modeling offers the only viable solution to evaluate complex problems met by the food industry and the food packaging supply chain:
- NIAS: non-intentionally added substances (no need for standards, analytical methods, hypothetical molecules can be accepted);
- cross-contamination between materials at any stage of the supply chain (all configurations can be included);
- post-consumer contaminations, including misuse
- optimization of decontamination step in mechanical recycling processes
- materials and articles with repeated use (no need for long experiments)
- materials and devices used with flows (no need of any setup)
- materials subjected to aging and long-term storage.
NIAS include hypothetical and unknown substances (e.g., breakdown products), but also known impurities and substances intentionally present or added to third-party materials (printed inks, adhesives, lacquers, overpackaging, secondary packaging). All the cases can be evaluated by combining molecular and migration modeling. The same approaches can be used to optimize decontamination conditions (solvent choice, temperature, duration) in recycling processes.
Test conditions for articles associated with repeated use and flows have not been detailed, and total migration scenarios prevail as a general recommendation in most of the regulations. Migration modeling can be used to evaluate articles and devices (gaskets, hoses, tubings, reservoirs, tanks, conveyors…) in more realistic conditions and all along their lifetime. As an illustration, plasticized materials are prone to release substances only for short-time contacts. Once the surface is depleted in plasticizer(s), the glass transition temperature increases sufficiently to transform the contact surface into a temporarily functional barrier. Any period without liquid in contact (e.g., stopping or cleaning period) redistributes the plasticizer(s) uniformly and causes a new risk of leaching.
Long-term storage of materials and material aging redistribute contaminants and may bring new breakdown products. Aging before use is not considered in current regulations. Modeling can offer a very cost-efficient method to evaluate the risk associated with the redistribution of contaminants from tie layers, printing inks, adhesives, lacquers before they are processed in food contact materials.
8.3 Bridging migration modeling, safe-by-design, and ecodesign approaches
This chapter encourages to address safety issues at early stages of the design of food packaging and food contact materials before even they become integrated into a finished product. Instead of checking the compliance on the finished product, additives, designs (shapes, surface-to-volume) and conditions of use (shelf-life, storage) can be used to minimize the risk of contamination and cross-contamination. Safe-by-design approaches181 are particularly relevant for food products devoted to babies and infants as well as for all applications maximizing the amount of recycled materials. The new generation of simulation tools200 will bridge safe-by-design approaches with eco-design, integrate 3D simulation of mass transfer and explicit food representation.
8.4 Online resources ease risk assessment
Safety decisions supported by calculations, modeling and simulation are only acceptable if they demonstrate that the migration amount, estimated by , is below the threshold, , prescribed by regulation, good manufacturing practices or other considerations. Otherwise, migration testing (experiments) must be applied. Without any threshold to compare, (i.e., non-evaluated substances), or its conversion into chronic exposure migration modeling loses its interest. The utility of migration increases when is not too much overestimated (i.e., too conservative) and when the value of is not the default value for a very toxic compound. The development of online resources (computational tools, databases, training, guidance,…) offers migration modeling and risk-assessment readily accessible, transparent, and cost-effective.
8.4.1 Lower bounds of toxicological thresholds for non-evaluated substances
For non-evaluated substances or in the absence of specific chemical data, the lowest (safest) value of is determined by the concept of toxicological threshold of concern (TTC)176. It has been recently endorsed jointly by EFSA and WHO201. It is pragmatic ersatz to identify situations, where migration can be presumed to present no appreciable human health risk (risk of cancer lower than 1 in one million). By excluding high potency carcinogens, i.e., aflatoxin-like, azoxy- or N-nitroso-compounds and benzidines, the TTC value for potentially genotoxic compounds reads:
Eq. relies on a chronic exposure estimate: the same food is in contact with the same packaging, and 1 kg (EU rule) or 3 kg (US rule) of food is daily consumed by an adult. For an adult of 60 kg (EU rule), the default value is 0.15 µg⋅kg-1 of food. The default value for infants (EU rule: infant up to 11 months old, weighing 5 kg and eating 0.75 kg) is 0.0167 µg⋅kg-1 of food. For infants under three months of age, additional considerations may be considered when values are close to , including metabolism, frequency, and duration of exposure.
Similar principles apply to substances, which are not part of the exclusionary categories and without structural alert of chemical-specific genotoxicity data suggesting a potential DNA reactivity. The values of and are tabulated in Table 10 for adults. The classification of substances relies on the Cramer decision tree 202, which has been implemented in the program Toxtree, commissioned by the JRC Computational Toxicology and Modelling, and in the OECD QSAR Toolbox. Both tools require chemical structures to be validated independently. Practical tools and databases are listed in Table 11.
Table 10. Thresholds concentration values based on approach for an adult of 60 kg and a daily intake of 1 kg.
| Type of value | in µg/kg body weight per day | in µg/kg food (assuming 1 kg daily intake) |
|---|---|---|
| With structural alter for genotoxicity | 0.0025 | 0.15 |
| organophosphates and carbamates | 0.3 | 18 |
| Cramer class III | 1.5 | 90 |
| Cramer class II | 9.0 | 540 |
| Cramer class I | 30 | 1800 |
Table 11. Main tools and databases to derive acceptable toxicological threshold.
| Type of tools | Online resources |
|---|---|
| TTC tools | OECD toolbox, Toxtree, TTC and related data and scientific opinion of EFSA |
| Toxicological databases | CEFIC LRI Toolbox including RepDose, FeDTex and CEMAS, Toxnet/ChemIdPlus , Cosmetic Ingredient Review (CIR) database and SCCS opinions, Council of Europe database (not publicly available), Euopean Chemicals Agency final decisions on compliance checks and testing proposals in REACH registration dossiers, Joint Research Centre ESIS database, GESTIS substance database for Occupational Exposure Limits (OELs), HPV-Program, IARC list of carcinogenic substances, NICNAS (Australia), NTP US/NIH list of carcinogenic substances, OSHA EU list of carcinogenic substances, Toxline from US NIH, TSCA from US EPA |
| General databases | Chemspider, PubChem |
8.4.2 Migration modeling tools
Several generations of tools have been developed during the last decades using either analytical or numerical schemes. All current tools are capable to describe transfer across multilayer structures and offer the possibility to simulate variable storage conditions (liquid contact, set-off, etc.). Similar results can be obtained with generic solvers of partial differential equations (PDE), such as ANSYS, Cast3M, Comsol Multiphysics®, Fluent™, FreeFem, Modelica, OpenFoam, etc. The difficulty for multilayer structures is the implementation of the internal conditions defined by Eq. XXX , which require a weak formulation of the PDE problem.
Table 12. Notable physics-based software and tools to evaluate migration.
| Type of tools | Description | License |
|---|---|---|
| Stand-alone compliance testing programs | Migratest© EXP, [AKTS-SML version 6][aktsml] | commercial (demo available) |
| Compliance testing client/server | Client-server SFPP3 application (SafeFoodPackaging portal version 3) to be used by one up to 25 simultaneous users. SFPP3 includes all public data of the European task force TF-MATHMOD. Interactive training on SFPP3 tools with case studies is available in French | freeware, partly open-source, online access or standalone installation. |
| Expandable preventive and safe-by-design tools | FMECAengine combined with key2key() language enabling to simulate supply chains, complex materials and applications (includes and expands all features implemented in SFPP3) | fully open-source (written in Matlab®, Octave language) |
| Online databases | Thermophysical properties of polymers; database of diffusion and partition coefficients of the European task force TF-MATHMOD | free access |
| Guidance | EU guidance, US guidance, generic guidance from INRA, Food Packaging Forum | free access |
| MOOC: Massive Open Online Course (USA) – 7 hours | MOOC lectures from the School of Packaging (Michigan State University) : overview, diffusion coefficients: , Partition coefficients: , Migration modeling and decision-making workshop | no registration |
| MOOC (EU) > 50 hours | The European project ERASMUS+ Fitness “Food packaging open courseware for higher education and staff of companies” is preparing a MOOC on all aspects of packaging design including compliance testing, food safety, and risk assessment: demo site | to be released by late 2019 |
The notable migration modeling software are listed in Table 12 with their corresponding license (open-source, freeware and commercial). It is worth noticing that they implement Fickian diffusion and that they assume uniform and isotropic distribution within each layer. These tools need to be combined with internal or external databases and mathematical relationships in order to take into account the nature of the migrant and the physical properties of the polymer. Open-source software and devoted programming language, as FMECAengine and key2key() language, are part of a global effort to foster interoperability, collaborative open-source projects and free templates for common problems. The European Committee for Standardization already identified that “a standardized terminology will improve future exchanges among experts in the entire area of materials modeling, facilitate the exchange with industrial end-users and experimentalists and reduce the barrier utilizing materials modeling” 203.
9 References
\1. ESA Outgassing data. http://esmat.esa.int/Services/outgassing_data/outgassing_data.html (access on Nov 22th 2018),
\2. NASA Outgassing Data for Selecting Spacecraft Materials. https://outgassing.nasa.gov/ (accessed on March 29, 2019),
\3. Kortenkamp, A.; Backhaus, T.; Faust, M. State of the Art Report on Mixture Toxicity - Final Report Executive Summary. 2009.
\4 Lee, D.-H. Evidence of the Possible Harm of Endocrine-Disrupting Chemicals in Humans: Ongoing Debates and Key Issues. Endocrinology and Metabolism (EnM) 2018, 33 (1), 44-52.
\5 Kortenkamp, A. Ten Years of Mixing Cocktails: A Review of Combination Effects of Endocrine-Disrupting Chemicals. Environmental Health Perspectives 2007, 115 (Suppl 1), 98-105.
\6 Wild, C. P. Complementing the Genome with an “Exposome”: The Outstanding Challenge of Environmental Exposure Measurement in Molecular Epidemiology. Cancer Epidemiology Biomarkers & Prevention 2005, 14 (8), 1847.
\7 Eicher, A.; Biedermann, M.; Zurfluh, M.; Grob, K. Migration by ‘direct’ or ‘indirect’ food contact? ‘Dry’ and ‘wetting’ foods? Experimental data for ‘touching’ contact of dry foods with paper and board. Food Additives & Contaminants: Part A 2015, 32 (1), 110-119.
\8 Muhamad, M. S.; Salim, M. R.; Lau, W. J.; Yusop, Z. A review on bisphenol A occurrences, health effects and treatment process via membrane technology for drinking water. Environmental Science and Pollution Research 2016, 23 (12), 11549-11567.
\9 Biedermann-Brem, S.; Biedermann, M.; Grob, K. Required barrier efficiency of internal bags against the migration from recycled paperboard packaging into food: a benchmark. Food Additives & Contaminants: Part A 2016, 33 (4), 725-740.
\10 Lommatzsch, M.; Richter, L.; Biedermann-Brem, S.; Biedermann, M.; Grob, K.; Simat, T. J. Functional barriers or adsorbent to reduce the migration of mineral oil hydrocarbons from recycled cardboard into dry food. European Food Research and Technology 2016, 242 (10), 1727-1733.
\11 Paul, U. C.; Fragouli, D.; Bayer, I. S.; Mele, E.; Conchione, C.; Cingolani, R.; Moret, S.; Athanassiou, A. Mineral oil barrier sequential polymer treatment for recycled paper products in food packaging. Materials Research Express 2017, 4 (1), 015501.
\12 Nriagu, J. O., Lead and Lead Poisoning in Antiquity. John Wiley: New-York, USA, 1983; p 437.
\13 Patterson, C. C.; Shirahata, H.; Ericson, J. E. Lead in ancient human bones and its relevance to historical developments of social problems with lead. Science of The Total Environment 1987, 61, 167-200.
\14 Delile, H.; Blichert-Toft, J.; Goiran, J.-P.; Keay, S.; Albarède, F. Lead in ancient Rome’s city waters. Proceedings of the National Academy of Sciences 2014, 111 (18), 6594.
\15 Doumerc, A.; de Leymarie, L., Législation française et étrangère concernant les falsifications alimentaires. Rueff et Cie, Editeurs: Paris, 1895; p 258.
\16 Hamel, G. T. Méfions-nous des conserves étrangères. La conserve alimentaire 1910, 19, 290-291.
\17 Rall, D. P. The Invisible Pollution. New England Journal of Medicine 1972, 287 (22), 1146-1147.
\18 Jaeger, R. J.; Rubin, R. J. Plasticizers from Plastic Devices: Extraction, Metabolism, and Accumulation by Biological Systems. Science 1970, 170 (3956), 460.
\19 Jaeger, R. J.; Rubin, R. J. Migration of a Phthalate Ester Plasticizer from Polyvinyl Chloride Blood Bags into Stored Human Blood and Its Localization in Human Tissues. New England Journal of Medicine 1972, 287 (22), 1114-1118.
\20 Lawrence, W. H.; Turner, J. E.; Autian, J. Reevaluation of plastic tubings currently used in medical and paramedical applications. Journal of Biomedical Materials Research 1969, 3 (2), 291-303.
\21 Kestel'man, V. N. e. a. The corrosion of polymeric material under the conditions of the microbiological synthesis of enzymes. Int. Biodetn Bull. 1972, 8 (1), 15-19.
\22 Figge, K. Migration of components from plastics-packaging materials into packed goods — test methods and diffusion models. Progress in Polymer Science 1980, 6 (4), 187-252.
\23 Giacin, J. R. EVALUATION OF PLASTICS PACKAGING MATERIALS FOR FOOD PACKAGING APPLICATIONS: FOOD SAFETY CONSIDERATIONS. Journal of Food Safety 1980, 2 (4), 257-276.
\24 Till, D. E.; Ehntholt, D. J.; Reid, R. C.; Schwartz, P. S.; Schwope, A. D.; Sidman, K. R.; Whelan, R. H. Migration of styrene monomer from crystal polystyrene to foods and food simulating liquids. Industrial & Engineering Chemistry Fundamentals 1982, 21 (2), 161-168.
\25 Till, D. E.; Ehntholt, D. J.; Reid, R. C.; Schwartz, P. S.; Sidman, K. R.; Schwope, A. D.; Whelan, R. H. Migration of BHT antioxidant from high density polyethylene to foods and food simulants. Industrial & Engineering Chemistry Product Research and Development 1982, 21 (1), 106-113.
\26 Schwope, A. D.; Till, D. E.; Ehntholt, D. J.; Sidman, K. R.; Whelan, R. H.; Schwartz, P. S.; Reid, R. C. Migration of BHT and Irganox 1010 from low-density polyethylene (LDPE) to foods and food-simulating liquids. Food and Chemical Toxicology 1987, 25 (4), 317-326.
\27 Schwope, A. D.; Till, D. E.; Ehntholt, D. J.; Sidman, K. R.; Whelan, R. H.; Schwartz, P. S.; Reid, R. C. Migration of Irganox 1010 from ethylene-vinyl acetate films to foods and food-simulating liquids. Food and Chemical Toxicology 1987, 25 (4), 327-330.
\28 Gandek, T. P., PhD Thesis. Migration of Phenolic Antioxidants from Polyolefins to Aqueous Media with Application to Indirect Food Additive Migration. Massachusetts Institute of Technology, Department of Chemical Engineering: Cambridge, MA, USA, 1986; p 519.
\29 Gandek, T. P.; Hatton, T. A.; Reid, R. C. Batch extraction with reaction: phenolic antioxidant migration from polyolefins to water. 1. Theory. Industrial & Engineering Chemistry Research 1989, 28 (7), 1030-1036.
\30 Gandek, T. P.; Hatton, T. A.; Reid, R. C. Batch extraction with reaction: phenolic antioxidant migration from polyolefins to water. 2. Experimental results and discussion. Industrial & Engineering Chemistry Research 1989, 28 (7), 1036-1045.
\31 Fornasiero, F.; Olaya, M. M.; Wagner, I.; Brüderle, F.; Prausnitz, J. M. Solubilities of nonvolatile solutes in polymers from molecular thermodynamics. AIChE Journal 2002, 48 (6), 1284-1291.
\32 Merrill, R. A. FOOD SAFETY REGULATION:Reforming the Delaney Clause. Annual Review of Public Health 1997, 18 (1), 313-340.
\33 National Research Council (US) Committee on Diet, N., and Cancer,, Diet, Nutrition, and Cancer. National Academies Press Washington, DC, USA, 1982; Vol. Available from: https://www.ncbi.nlm.nih.gov/books/NBK216644/, p 496.
\34 Roberts, H. R. Food Additives - A Study in the Evolution of Safety. Food Drug Cosmetic Law Journal 1976, 31, 404.
\35 EC. Commission Directive 90/128/EEC of 23 February 1990 relating to plastic materials and articles intended to come into contact with foodstuffs. Official Journal of the European Union 1990, L75, 19-40.
\36 EC. Commission Directive 2002/72/EC of 6 August 2002 relating to plastic materials and articles intended to come into contact with foodstuffs. Official Journal of the European Union 2002, L220, 18-56.
\37 EC. Commission Regulation (EU) No 10/2011 of 14 January 2011 on plastic materials and articles intended to come into contact with food Text with EEA relevance. Official Journal of the European Union 2011, L12, 1-89.
\38 CFDA. National Standard of The People’s Republic Of China GB 9685-2016: National Food Safety Standard Standard for Uses of Additives in Food Contact Materials and Their Products. National Health and Family Planning Commission 2016, Available from: http://samr.cfda.gov.cn/WS01/CL0087/166631.html.
\39 FDA. Inventory of Effective Food Contact Substance (FCS) Notifications. 2018, available from: https://www.fda.gov/food/ingredientspackaginglabeling/packagingfcs/notifications/default.htm.
\40 DGCCRF. Arrêté du 9 novembre 1994 relatif aux matériaux et objets en caoutchouc au contact des denrées, produits et boissons alimentaires. Journal Officiel de la République Française 1995, (2 décembre 1994), 17029-17035.
\41 EuPIA Good Manufacturing Practice (GMP) Printing Inks for Food Contact Materials, 4th completely revised version, EuPIA, March 2016. http://www.eupia.org/index.php?id=29 ((access on March 29, 2019)),
\42 EDI Swiss Ordinance of the FDHA on materials and articles intended to come into contact with foodstuffs (SR 817.023.21) , Eidgenössisches Departement des Innern (EDI), 16.12.2016. https://www.admin.ch/opc/de/classified-compilation/20143393/index.html ((accessed on March 29, 2019)),
\43 EuPIA EuPIA Guidance for Risk Assessment of Non-Intentionally Added Substances (NIAS) and Non-Listed Substances (NLS) in printing inks for food contact materials. http://www.eupia.org/uploads/tx_edm/2016-02-24_EuPIA_Info_Note_Inks_and_Coatings_for_High_Temperature_Applications.pdf (accessed on March 29, 2019),
\44 COE Paper and board materials and articles intended to come into contact with foodstuffs - version 4 - 12.02.2009 - https://rm.coe.int/16804e4794; 2009; p 148.
\45 CEPI Industry Guideline for the Compliance of Paper & Board Materials and Articles for Food Contact. Issue 2 September 2012 - http://www.cepi.org/system/files/public/documents/publications/foodcontact/2012/Industry%20guideline-updated2012final.pdf; Confederation of European Paper Industries: Brussels, Belgium, 2012; p 30.
\46 BfR XXXVI. Papiere, Kartons und Pappen für den Lebensmittelkontakt - https://bfr.ble.de/kse/faces/resources/pdf/360.pdf; BfR: Berlin, Gemany, 2017; p 16.
\47 EFSA. Scientific Opinion on Mineral Oil Hydrocarbons in Food. EFSA Journal 2012, 10 (6), 2704 (185 p).
\48 Bradley, E. L.; Burden, R. A.; Bentayeb, K.; Driffield, M.; Harmer, N.; Mortimer, D. N.; Speck, D. R.; Ticha, J.; Castle, L. Exposure to phthalic acid, phthalate diesters and phthalate monoesters from foodstuffs: UK total diet study results. Food Additives & Contaminants: Part A 2013, 30 (4), 735-742.
\49 Bradley, E. L.; Burden, R. A.; Leon, I.; Mortimer, D. N.; Speck, D. R.; Castle, L. Determination of phthalate diesters in foods. Food Additives & Contaminants: Part A 2013, 30 (4), 722-734.
\50 MAFF, U. Phthalates in paper and board packaging. MAFF Food Surveillance Information Sheet. 1995, Number 60.
\51 MAFF, U. Phthalates in food. MAFF Food Surveillance Information Sheet. 1996, Number 82, https://webarchive.nationalarchives.gov.uk/20081230231745/http://archive.food.gov.uk/maff/archive/food/infsheet/1996/no82/82phthal.htm.
\52 MAFF, U. Phthalates in infant formulae. MAFF Food Surveillance Information Sheet. 1996, Number 83.
\53 MAFF, U. Phthalates in infant formulae – follow-up survey. MAFF Food Surveillance Information Sheet. 1998, Number 168.
\54 EFSA. Opinion of the Scientific Panel on food additives, flavourings, processing aids and materials in contact with food (AFC) related to 2,2-bis(4-hydroxyphenyl)propane bis(2,3-epoxypropyl)ether (Bisphenol A diglycidyl ether, BADGE). REF. No 13510 and 39700. EFSA Journal 2004, 2 (7), 86.
\55 Six, T.; Feigenbaum, A.; Riquet, A. M. Mechanism of migration from agglomerated cork stoppers: I. An electron spin resonance investigation. Journal of Applied Polymer Science 2002, 83 (12), 2644-2654.
\56 Six, T.; Feigenbaum, A. Mechanism of migration from agglomerated cork stoppers. Part 2: Safety assessment criteria of agglomerated cork stoppers for champagne wine cork producers, for users and for control laboratories. Food Additives & Contaminants 2003, 20 (10), 960-971.
\57 Campanella, G.; Ghaani, M.; Quetti, G.; Farris, S. On the origin of primary aromatic amines in food packaging materials. Trends in Food Science & Technology 2015, 46 (1), 137-143.
\58 Mutsuga, M.; Yamaguchi, M.; Kawamura, Y. Quantification of isocyanates and amines in polyurethane foams and coated products by liquid chromatography–tandem mass spectrometry. Food Science & Nutrition 2014, 2 (2), 156-163.
\59 Athenstädt, B.; Fünfrocken, M.; Schmidt, T. C. Migrating components in a polyurethane laminating adhesive identified using gas chromatography/mass spectrometry. Rapid Communications in Mass Spectrometry 2012, 26 (16), 1810-1816.
\60 Castle, L.; Sharman, M.; Gilbert, J. Gas chromatographic-mass spectrometric determination of epoxidized soybean oil contamination of foods by migration from plastic packaging. Journal - Association of Official Analytical Chemists 1988, 71 (6), 1183-6.
\61 EC 4-Nonylphenol (branched) and nonylphenol - Risk Assessment - EUR 20387 EN - https://www.bfr.bund.de/cm/343/4_nonylphenol_und_nonylphenol.pdf; EUR 20387 EN; European Communities: Luxembourg, 2002; p 14.
\62 EC. DIRECTIVE 2003/53/EC OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 18 June 2003 amending for the 26th time Council Directive 76/769/EEC relating to restrictions on the marketing and use of certain dangerous substances and preparations (nonylphenol, nonylphenol ethoxylate and cement). Official Journal of the European Union 2003, L178, 24-27.
\63 ECHA. Entry 46: Nonylphenol - Conditions of restriction. Annex XVII - Restrictions on the manufacture, placing on the market and use of certain dangerous substances, mixtures and articles 2016, https://echa.europa.eu/fr/substances-restricted-under-reach/-/dislist/details/0b0236e1807e2b6e.
\64 EFSA. Opinion of the Scientific Panel on food additives, flavourings, processing aids and materials in contact with food (AFC) related to Semicarbazide in food. EFSA Journal 2005, 3 (6), 219.
\65 Stadler, R. H.; Mottier, P.; Guy, P.; Gremaud, E.; Varga, N.; Lalljie, S.; Whitaker, R.; Kintscher, J.; Dudler, V.; Read, W. A.; Castle, L. Semicarbazide is a minor thermal decomposition product of azodicarbonamide used in the gaskets of certain food jars. Analyst 2004, 129 (3), 276-281.
\66 EC. Commission Directive 2004/1/EC of 6 January 2004 amending Directive 2002/72/EC as regards the suspension of the use of azodicarbonamide as blowing agent (Text with EEA relevance). Official Journal of the European Union 2004, C007, 45-46.
\67 EFSA. Opinion of the Scientific Panel on food additives, flavourings, processing aids and materials in contact with food (AFC) related to 2-Isopropyl thioxanthone (ITX) and 2-ethylhexyl-4-dimethylaminobenzoate (EHDAB) in food contact materials. EFSA Journal 2005, 3 (12), 293.
\68 Johns, S. M.; Gramshaw, J. W.; Castle, L.; Jickells, S. M. Studies on functional barriers to migration. 1. Transfer of benzophenone from printed paperboard to microwaved food. Deutsche Lebensmittel-Rundschau 1995, 91 (3), 69-73.
\69 EFSA. Opinion of the Scientific Panel on food additives, flavourings, processing aids and materials in contact with food (AFC) related to 2,2-BIS(4-HYDROXYPHENYL)PROPANE. EFSA Journal 2006, 5 (1), 428.
\70 Gundert-Remy, U.; Bodin, J.; Bosetti, C.; FitzGerald, R.; Hanberg, A.; Hass, U.; Hooijmans, C.; Rooney, A. A.; Rousselle, C.; van Loveren, H.; Wölfle, D.; Barizzone, F.; Croera, C.; Putzu, C.; Castoldi, A. F. Bisphenol A (BPA) hazard assessment protocol. EFSA Supporting Publications 2017, 14 (12), 1354E.
\71 Castle, L.; Kelly, M.; Gilbert, J. Migration of mineral hydrocarbons into foods. 2. Polystyrene, ABS, and waxed paperboard containers for dairy products. Food Additives and Contaminants 1993, 10 (2), 167-174.
\72 EFSA. Scientific Opinion on Mineral Oil Hydrocarbons in Food. EFSA Journal 2012, 10 (6), 2704.
\73 EC. Rapid Alert System for Food and Feed - RASFF. https://webgate.ec.europa.eu/rasff-window/portal/index.cfm?event=notificationsList (accessed on Dec 31, 2018),
\74 Begley, T. H. Methods and approaches used by FDA to evaluate the safety of food packaging materials. Food Additives & Contaminants 1997, 14 (6-7), 545-553.
\75 Limm, W.; Hollifield, H. C. Modelling of additive diffusion in polyolefins. Food Additives & Contaminants 1996, 13 (8), 949-967.
\76 Baner, A.; Brandsch, J.; Franz, R.; Piringer, O. The application of a predictive migration model for evaluating the compliance of plastic materials with European food regulations. Food Additives & Contaminants 1996, 13 (5), 587-601.
\77 Baner, A.; Franz, R.; Piringer, O. Alternative methods for the determination and evaluation of migration potential from polymeric food contact materials. Deutsche Lebensmittel-Rundschau 1994, 90 (6), 181-185.
\78 Baner, A.; Franz, R.; Piringer, O. Alternative methods for the determination and evaluation of migration potential from polymeric food contact materials. Deutsche Lebensmittel-Rundschau 1994, 90 (5), 137-143.
\79 K., H.; O., P. Evaluation of migration models to used under Directive 90/128/EEC. Final report contract SMT4-CT98-7513 - EUR 20604 EN - https://publications.europa.eu/en/publication-detail/-/publication/07919045-cba5-4ad2-9460-c17c56e2f329/language-en; European Commission, Directorate General for Research: Luxembourg, 2002; p 249.
\80 Hoekstra, E.; Brandsch, R.; Dequatre, C.; Mercea, P.; Milana, M. R.; Stoermer, A.; Trier, X.; Vitrac, O.; Schaefer, A.; Simoneau, C. Practical guidelines on the application of migration modelling for the estimation of specific migration; European Commission, Joint Research Centre, Institute for Health and Consumers Protection: 2015.
\81 Schwope, A. D.; Goydan, R.; Reid, R. Methodology for Estimating the Migration of Additives and Impurities from Polymeric Materials - EPA 560/5-85-015; Office of Pesticides and Toxic Substances, U.S. Environmental Protection Agency (EPA): Washington DC, USA - https://nepis.epa.gov/Exe/ZyPURL.cgi?Dockey=P100BCMB.TXT, 1990; p 148.
\82 Vitrac, O. An atomistic Flory-Huggins formulation for the tailored prediction of activity and partition coefficients. https://mediaspace.msu.edu/media/Dr.+Olivier+Vitrac+presentsA+An+atomistic+Flory-Huggins+formulation+for+the+tailored+prediction+of+activity+and+partition+coefficients/1_uzi6h91k (accessed on Dec 31, 2019),
\83 Vitrac, O. Diffusion coefficients of organic solutes in polymers: new perspectives of prediction. https://mediaspace.msu.edu/media/Dr.+Olivier+Vitrac+presentsA+Diffusion+coefficients+of+organic+solutes+in+polymersA/1_zz20dgt9 (accessed on Dec 31, 2019),
\84 Vitrac, O. New computational methodologies as enablers of safer food contact articles. https://www.youtube.com/watch?v=v1SMAUy6XJs&t=312s (accessed on Dec 31, 2018),
\85 Vergnaud, J. M., Liquid transport processes in polymeric materials: modeling and industrial applications. Prentice Hall International LTD: London, UK, 1991; p 362.
\86 Piringer, O. G.; Baner, A. L., Plastic packaging materials for food: barrier function, mass transport, quality assurance, and legislation. Wiley-VCH Verlag: Weinheim, Germany, 2000; p 576.
\87 Barnes, K.; Sinclair, R.; Watson, D., Chemical Migration and Food Contact Materials. CRC Press LCL: Boca-Raton, FL, USA, 2006; p 464.
\88 Vergnaud, J. M.; Rosca, I. D., Assessing Food Safety of Polymer Packaging. Rapra Technology: Shawbury, UK, 2006; p 273.
\89 Piringer, O. G.; Baner, A. L., Plastic Packaging Interactions with Food and Pharmaceuticals. Wiley-VCH Verlag: Weinheim, Germany, 2008; p 614.
\90 Singh, P.; Wani, A. A.; Langowski, H. C., Food Packaging Materials: Testing & Quality Assurance. CRC Press: Boca-Raton, USA, 2017; p 344.
\91 Poças, M. F.; Oliveira, J. C.; Oliveira, F. A. R.; Hogg, T. A Critical Survey of Predictive Mathematical Models for Migration from Packaging. Critical Reviews in Food Science and Nutrition 2008, 48 (10), 913-928.
\92 Helmroth, E.; Rijk, R.; Dekker, M.; Jongen, W. Predictive modelling of migration from packaging materials into food products for regulatory purposes. Trends in Food Science & Technology 2002, 13 (3), 102-109.
\93 Arvanitoyannis, I. S.; Bosnea, L. Migration of substances from food packaging materials to foods. Critical Reviews in Food Science and Nutrition 2004, 44 (2), 63-76.
\94 Lau, O.-W.; Wong, S.-K. Contamination in food from packaging material. Journal of Chromatography A 2000, 882 (1–2), 255-270.
\95 Gillet, G.; Vitrac, O.; Tissier, D.; Saillard, P.; Desobry, S. Development of decision tools to assess migration from plastic materials in contact with food. Food Additives and Contaminants Part a-Chemistry Analysis Control Exposure & Risk Assessment 2009, 26 (12), 1556-1573.
\96 Vitrac, O.; Challe, B.; Leblanc, J. C.; Feigenbaum, A. Contamination of packaged food by substances migrating from a direct-contact plastic layer: Assessment using a generic quantitative household scale methodology. Food Additives & Contaminants 2007, 24 (1), 75-94.
\97 Vitrac, O.; Leblanc, J.-C. Consumer exposure to substances in plastic packaging. I. Assessment of the contribution of styrene from yogurt pots. Food Additives and Contaminants 2007, 24 (2).
\98 Vitrac, O.; Hayert, M., Design of safe packaging materials under uncertainty. In Chemical Engineering Research Trends, Berton, L. P., Ed. Nova Science Publishers: New-York, USA, 2007; pp 251-292.
\99 Robertson, G. L., Food Packaging: Principles and Practice, Third Edition. CRC Press: Boca-Raton, USA, 2016; p 686.
\100 Cussler, E. L., Diffusion: Mass Transfer in Fluid Systems. 3rd Edition. Cambridge University Press: Cambridge, UK, 2009; p 631.
\101 Vieth, W. R., Diffusion in and Through Polymers: Principles and Applications. Carl Hanser GmbH: Munich, Germany, 1991; p 330.
\102 Crank, J., The Mathematics of Diffusion Oxford University Press: Bristol, UK, 1975; p 414.
\103 Stastna, J.; De Kee, D., Transport Properties in Polymers. CRC Press: Boca-Raon, USA, 1995; p 303.
\104 Mehrer, H., Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes. Springer-Verlag: Heidelberg, Germany, 2010.
\105 Neogi, P., Diffusion in Polymers. Marcel Dekker, Inc: New-Yourk, USA, 1996.
\106 Ben-Naim, A. Y., Solvation Thermodynamics. Springer Science: New-York, USA, 2013; p 246.
\107 Vrentas, J. S.; Vrentas, C. M., Diffusion and Mass Transfer. CRC Press: Boca-Raton, FL, USA, 2013; p 619.
\108 EC. COMMISSION DECISION of 28 January 1997 establishing the identification system for packaging materials pursuant to European Parliament and Council Directive 94/62/EC on packaging and packaging waste (97/ 129/EC). Official Journal of the European Communities 1997, L50, 28-31.
\109 GB. GB/T 16288-2008 : Marking of Plastics Products. NATIONAL STANDARD OF THE PEOPLE’S REPUBLIC OF CHINA 2008, (ICS 83. 140, Y 28), 1-17.
\110 van Krevelen, D. W.; te Nijenhuis, K., Properties of Polymers: Their Correlation with Chemical Structure; their Numerical Estimation and Prediction from Additive Group Contributions. Elsevier Science: Amsterdam, NL, 2009.
\111 Chemical Retrieval on the Web Polymer Properties Database. http://polymerdatabase.com/ (accessed on March 31, 2019),
\112 Gillet, G.; Vitrac, O.; Desobry, S. Prediction of Solute Partition Coefficients between Polyolefins and Alcohols Using a Generalized Flory−Huggins Approach. Industrial & Engineering Chemistry Research 2009, 48 (11), 5285-5301.
\113 Gillet, G.; Vitrac, O.; Desobry, S. A Fast Method to Assess the Composition of a Polyolefin: An Application to Compliance Testing of Food Contact Materials. Journal of Applied Polymer Science 2011, 119 (3), 1492-1515.
\114 Nguyen, P.-M.; Lyathaud, C.; Vitrac, O. A two-scale pursuit method for the tailored identification and quantification of unknown polymer additives and contaminants by 1H NMR. Industrial & Engineering Chemistry Research 2015, 54 (10), 2667-2681.
\115 Masood, S. H.; KeshavaMurthy, V. Development of collapsible PET water fountain bottles. Journal of Materials Processing Technology 2005, 162-163, 83-89.
\116 Huang, H.-H.; Chen, L.-W.; Lu, W.-H.; Lin, W.-C.; Chen, Y.-C. Design and Simulation Analysis of Lightweight HDPE Milk Bottle. Polymers and Polymer Composites 2018, 26 (1), 91-98.
\117 Hu, Q. C.; Sha, W. J.; Li, Y. H.; Wang, Y. S. Structural Optimization and Lightweight Design of PET Bottle Based on ABAQUS. Advanced Materials Research 2012, 346, 558-563.
\118 Demirel, B.; Daver, F. The effects on the properties of PET bottles of changes to bottle-base geometry. Journal of Applied Polymer Science 2009, 114 (6), 3811-3818.
\119 Roe, R.-J.; Bair, H. E.; Gieniewski, C. Solubility and diffusion coefficient of antioxidants in polyethylene. Journal of Applied Polymer Science 1974, 18 (3), 843-856.
\120 Moisan, J. Y. Diffusion des additifs du polyethylene—I: Influence de la nature du diffusant. European Polymer Journal 1980, 16 (10), 979-987.
\121 Ju, S. T.; Duda, J. L.; Vrentas, J. S. Influence of temperature on the diffusion of solvents in polymers above the glass transition temperature. Industrial & Engineering Chemistry Product Research and Development 1981, 20 (2), 330-335.
\122 Ehlich, D.; Sillescu, H. Tracer diffusion at the glass transition. Macromolecules 1990, 23 (6), 1600-1610.
\123 Mauritz, K. A.; Storey, R. F.; George, S. E. A general free volume-based theory for the diffusion of large molecules in amorphous polymers above the glass temperature. I. Application to di-n-alkyl phthalates in PVC. Macromolecules 1990, 23 (2), 441-450.
\124 Arnould, D.; Laurence, R. L. Size effects on solvent diffusion in polymers. Industrial & Engineering Chemistry Research 1992, 31 (1), 218-228.
\125 Griffiths, M. C.; Strauch, J.; Monteiro, M. J.; Gilbert, R. G. Measurement of Diffusion Coefficients of Oligomeric Penetrants in Rubbery Polymer Matrixes. Macromolecules 1998, 31 (22), 7835-7844.
\126 Hall, D. B.; Hamilton, K. E.; Miller, R. D.; Torkelson, J. M. Translational and Rotational Diffusion of Probe Molecules in Polymer Films near Tg: Effect of Hydrogen Bonding. Macromolecules 1999, 32 (24), 8052-8058.
\127 Vitrac, O.; Hayert, M. Identification of Diffusion Transport Properties from Desorption/Sorption Kinetics: An Analysis Based on a New Approximation of Fick Equation during Solid−Liquid Contact. Industrial & Engineering Chemistry Research 2006, 45 (23), 7941-7956.
\128 von Meerwall, E. D.; Lin, H.; Mattice, W. L. Trace Diffusion of Alkanes in Polyethylene: Spin-Echo Experiment and Monte Carlo Simulation. Macromolecules 2007, 40 (6), 2002-2007.
\129 Grabowski, C. A.; Mukhopadhyay, A. Size Effect of Nanoparticle Diffusion in a Polymer Melt. Macromolecules 2014, 47 (20), 7238-7242.
\130 Vagias, A.; Schultze, J.; Doroshenko, M.; Koynov, K.; Butt, H.-J.; Gauthier, M.; Fytas, G.; Vlassopoulos, D. Molecular Tracer Diffusion in Nondilute Polymer Solutions: Universal Master Curve and Glass Transition Effects. Macromolecules 2015, 48 (24), 8907-8912.
\131 Begley, T.; Castle, L.; Feigenbaum, A.; Franz, R.; Hinrichs, K.; Lickly, T.; Mercea, P.; Milana, M.; O’Brien, A.; Rebre, S.; Rijk, R.; Piringer, O. Evaluation of migration models that might be used in support of regulations for food-contact plastics AU - Begley, T. Food Additives & Contaminants 2005, 22 (1), 73-90.
\132 Hong, S.-U. Predicting ability of free-volume theory for solvent self-diffusion coefficients in rubbers. Journal of Applied Polymer Science 1996, 61 (5), 833-841.
\133 Vrentas, J. S.; Vrentas, C. M. Predictive methods for self-diffusion and mutual diffusion coefficients in polymer–solvent systems. European Polymer Journal 1998, 34 (5–6), 797-803.
\134 Vrentas, J. S.; Vrentas, C. M.; Faridi, N. Effect of Solvent Size on Solvent Self-Diffusion in Polymer−Solvent Systems. Macromolecules 1996, 29 (9), 3272-3276.
\135 Zielinski, J. M.; Duda, J. L. Predicting polymer/solvent diffusion coefficients using free-volume theory. AIChE Journal 1992, 38 (3), 405-415.
\136 Fang, X.; Vitrac, O. Predicting diffusion coefficients of chemicals in and through packaging materials. Critical Reviews in Food Science and Nutrition 2017, 57 (2), 275-312.
\137 Karlsson, G. E.; Johansson, T. S.; Gedde, U. W.; Hedenqvist, M. S. Determining Limonene Diffusion in Molten Polyethylene from within 0.1 μs Molecular Dynamics Trajectories. Macromolecules 2002, 35 (19), 7453-7459.
\138 Vitrac, O.; Lézervant, J.; Feigenbaum, A. Decision trees as applied to the robust estimation of diffusion coefficients in polyolefins. Journal of Applied Polymer Science 2006, 101 (4), 2167-2186.
\139 Harmandaris, V. A.; Adhikari, N. P.; van der Vegt, N. F. A.; Kremer, K.; Mann, B. A.; Voelkel, R.; Weiss, H.; Liew, C. Ethylbenzene Diffusion in Polystyrene: United Atom Atomistic/Coarse Grained Simulations and Experiments. Macromolecules 2007, 40 (19), 7026-7035.
\140 Durand, M.; Meyer, H.; Benzerara, O.; Baschnagel, J.; Vitrac, O. Molecular dynamics simulations of the chain dynamics in monodisperse oligomer melts and of the oligomer tracer diffusion in an entangled polymer matrix. Journal of Chemical Physics 2010, 132 (19), 194902.
\141 Gautieri, A.; Vesentini, S.; Redaelli, A. How to predict diffusion of medium-sized molecules in polymer matrices. From atomistic to coarse grain simulations. Journal of Molecular Modeling 2010, 16 (12), 1845-1851.
\142 Lin, E.; You, X.; Kriegel, R. M.; Moffitt, R. D.; Batra, R. C. Atomistic to coarse grained simulations of diffusion of small molecules into polymeric matrix. Computational Materials Science 2017, 138, 448-461.
\143 Hoekstra, E.; Brandsch, R.; Dequatre, C.; Mercea, P.; Milana, M. R.; Stoermer, A.; Trier, X.; Vitrac, O.; Schaefer, A.; Simoneau, C. Practical guidelines on the application of migration modelling for the estimation of specific migration - EUR 27529 EN - https://ec.europa.eu/jrc/en/publication/practical-guidelines-application-migration-modelling-estimation-specific-migration; 2015; p 36.
\144 Kirkwood, J. G.; Buff, F. P. The Statistical Mechanical Theory of Solutions. I. The Journal of Chemical Physics 1951, 19 (6), 774-777.
\145 Flory, P. J. Thermodynamics of High Polymer Solutions. The Journal of Chemical Physics 1942, 10 (1), 51-61.
\146 Flory, P. J. The Configuration of Real Polymer Chains. The Journal of Chemical Physics 1949, 17 (3), 303-310.
\147 Flory, P. J., Principles of Polymer Chemistry. Cornell University Press: Iathaca, NY, USA, 1953.
\148 Kadam, A.; Karbowiak, T.; Voilley, A.; Bellat, J.-P.; Vitrac, O.; Debeaufort, F. Sorption of n-hexane in amorphous polystyrene. Journal of Polymer Science Part B: Polymer Physics 2014, 52 (19), 1252-1258.
\149 Hansen, C. M., Hansen Solubility Parameters: A User's Handbook, Second Edition. CRC Press: Boca-Raton, FL, USA, 2007; p 519.
\150 Baner, A. L.; Piringer, O. G. Prediction of solute partition coefficients between polyolefins and alcohols using the regular solution theory and group contribution methods. Industrial & Engineering Chemistry Research 1991, 30 (7), 1506-1515.
\151 Kontogeorgis, G. M.; Folas, G. K., Thermodynamic Models for Industrial Applications: From Classical and Advanced Mixing Rules to Association Theories. John Wiley & Sons Ltd: Chichester, UK, 2009; p 692.
\152 De Angelis, M. G.; Boulougouris, G. C.; Theodorou, D. N. Prediction of Infinite Dilution Benzene Solubility in Linear Polyethylene Melts via the Direct Particle Deletion Method. The Journal of Physical Chemistry B 2010, 114 (19), 6233-6246.
\153 Boulougouris, G. C. On the Estimation of the Free Energy, From a Single Equilibrium Statistical Ensemble, via Particle Reinsertion. The Journal of Physical Chemistry B 2011, 116 (3), 997-1006.
\154 Boulougouris, G. C. Calculation of the Chemical Potential beyond the First-Order Free-Energy Perturbation: From Deletion to Reinsertion†. Journal of Chemical & Engineering Data 2010, 55 (10), 4140-4146.
\155 Özal, T. A.; Peter, C.; Hess, B.; van der Vegt, N. F. A. Modeling Solubilities of Additives in Polymer Microstructures: Single-Step Perturbation Method Based on a Soft-Cavity Reference State. Macromolecules 2008, 41 (13), 5055-5061.
\156 Hess, B.; van der Vegt, N. F. A. Predictive Modeling of Phenol Chemical Potentials in Molten Bisphenol A−Polycarbonate over a Broad Temperature Range. Macromolecules 2008, 41 (20), 7281-7283.
\157 Hess, B.; Peter, C.; Ozal, T.; van der Vegt, N. F. A. Fast-Growth Thermodynamic Integration: Calculating Excess Chemical Potentials of Additive Molecules in Polymer Microstructures. Macromolecules 2008, 41 (6), 2283-2289.
\158 Gillet, G.; Vitrac, O.; Desobry, S. Prediction of Partition Coefficients of Plastic Additives between Packaging Materials and Food Simulants. Industrial & Engineering Chemistry Research 2010, 49 (16), 7263-7280.
\159 Vitrac, O.; Gillet, G. An Off-Lattice Flory-Huggins Approach of the Partitioning of Bulky Solutes between Polymers and Interacting Liquids. International Journal of Chemical Reactor Engineering 2010, 8.
\160 Nguyen, P.-M.; Guiga, W.; Dkhissi, A.; Vitrac, O. Off-lattice Flory-Huggins approximations for the tailored calculation of activity coefficients of organic solutes in random and block copolymers. Industrial & Engineering Chemistry Research 2017, 56 (3), 774–787.
\161 Nguyen, P.-M.; Guiga, W.; Vitrac, O. Molecular thermodynamics for food science and engineering. Food Research International 2017, 88, Part A, 91-104.
\162 Tribble, A., Fundamentals of Contamination Control. SPIE Press: Washington, DC, USA, 2000; p 174.
\163 Lee, G. Materials for ultra-high vacuum. . Illinois 1989.
\164 Weissler, G.; Carlson, R., Vacuum Physics and Technology. Academic Press: New York, 1979.
\165 Alexander Stern, S. Polymers for gas separations: the next decade. Journal of Membrane Science 1994, 94 (1), 1-65.
\166 Klopffer, M. H.; Flaconneche, B. Transport properties of gases in polymers: Bibliographic review. Oil Gas Sci. Technol. 2001, 56 (3), 223-244.
\167 Masaro, L.; Zhu, X. X. Physical models of diffusion for polymer solutions, gels and solids. Progress in Polymer Science 1999, 24 (5), 731-775.
\168 Pigeonneau, F.; Jaffrennou, B.; Letailleur, A.; Limouzin, K. Numerical investigation of generalized Graetz problem in circular tube with a mass transfer coupling between the solid and the liquid. International Journal of Heat and Mass Transfer 2016, 96, 381-395.
\169 Gao, S.; Wang, Z.-W.; Hu, C.-Y.; Wu, Y.-M. Investigation of Migration Model of Printing Inks on Paper Packaging. Journal of Food Process Engineering 2014, 37 (2), 146-159.
\170 Aparicio, J. L.; Elizalde, M. Migration of Photoinitiators in Food Packaging: A Review. Packaging Technology and Science 2015, 28 (3), 181-203.
\171 Salafranca, J.; Clemente, I.; Isella, F.; Nerín, C.; Bosetti, O. Influence of oxygen and long term storage on the profile of volatile compounds released from polymeric multilayer food contact materials sterilized by gamma irradiation. Analytica Chimica Acta 2015, 878, 118-130.
\172 Szendi, K.; Gyöngyi, Z.; Kontár, Z.; Gerencsér, G.; Berényi, K.; Hanzel, A.; Fekete, J.; Kovács, A.; Varga, C. Mutagenicity and Phthalate Level of Bottled Water Under Different Storage Conditions. Exposure and Health 2018, 10 (1), 51-60.
\173 Careghini, A.; Mastorgio, A. F.; Saponaro, S.; Sezenna, E. Bisphenol A, nonylphenols, benzophenones, and benzotriazoles in soils, groundwater, surface water, sediments, and food: a review. Environmental Science and Pollution Research 2015, 22 (8), 5711-5741.
\174 Spack, L. W.; Leszczyk, G.; Varela, J.; Simian, H.; Gude, T.; Stadler, R. H. Understanding the contamination of food with mineral oil: the need for a confirmatory analytical and procedural approach. Food Additives & Contaminants: Part A 2017, 34 (6), 1052-1071.
\175 FDA. Food Additives; Threshold of Regulation for Substances Used in Food-Contact Articles. Federal Register 1995, 60 (136), 36582-36596.
\176 Kroes, R.; Renwick, A. G.; Cheeseman, M.; Kleiner, J.; Mangelsdorf, I.; Piersma, A.; Schilter, B.; Schlatter, J.; van Schothorst, F.; Vos, J. G.; Würtzen, G. Structure-based thresholds of toxicological concern (TTC): guidance for application to substances present at low levels in the diet. Food and Chemical Toxicology 2004, 42 (1), 65-83.
\177 Sagiv, A. Exact solution of mass diffusion into a finite volume. Journal of Membrane Science 2001, 186 (2), 231-237.
\178 Sagiv, A. Theoretical formulation of the diffusion through a slab—theory validation. Journal of Membrane Science 2002, 199 (1), 125-134.
\179 Goujot, D.; Vitrac, O. Extension to nonlinear adsorption isotherms of exact analytical solutions to mass diffusion problems. Chemical Engineering Science 2013, 99, 2-22.
\180 Feigenbaum, A.; Dole, P.; Aucejo, S.; Dainelli, D.; Garcia, C. D. L. C.; Hankemeier, T.; N'Gono, Y.; Papaspyrides, C. D.; Paseiro, P.; Pastorelli, S.; Pavlidou, S.; Pennarun, P. Y.; Saillard, P.; Vidal, L.; Vitrac, O.; Voulzatis, Y. Functional barriers: Properties and evaluation AU - Feigenbaum, A. Food Additives & Contaminants 2005, 22 (10), 956-967.
\181 Nguyen, P.-M.; Goujon, A.; Sauvegrain, P.; Vitrac, O. A Computer-Aided Methodology to Design Safe Food Packaging and Related Systems. Aiche Journal 2013, 59 (4), 1183-1212.
\182 Vitrac, O.; Hayert, M. Effect of the distribution of sorption sites on transport diffusivities: A contribution to the transport of medium-weight-molecules in polymeric materials. Chemical Engineering Science 2007, 62 (9), 2503-2521.
\183 Courgneau, C.; Vitrac, O.; Ducruet, V.; Riquet, A.-M. Local demixion in plasticized polylactide probed by electron spin resonance. Journal of Magnetic Resonance 2013, 233, 37-48.
\184 Vrentas, J. S.; Vrentas, C. M. A new equation relating self-diffusion and mutual diffusion coefficients in polymer-solvent systems. Macromolecules 1993, 26 (22), 6129-6131.
\185 Fang, X.; Domenek, S.; Ducruet, V.; Refregiers, M.; Vitrac, O. Diffusion of Aromatic Solutes in Aliphatic Polymers above Glass Transition Temperature. Macromolecules 2013, 46 (3), 874-888.
\186 Ewender, J.; Welle, F. Determination of the activation energies of diffusion of organic molecules in poly(ethylene terephthalate). Journal of Applied Polymer Science 2013, 128 (6), 3885-3892.
\187. Welle, F. A new method for the prediction of diffusion coefficients in poly(ethylene terephthalate). Journal of Applied Polymer Science 2013, 129 (4), 1845-1851.
\188. Ewender, J.; Welle, F. Determination and Prediction of the Lag Times of Hydrocarbons through a Polyethylene Terephthalate Film. Packaging Technology and Science 2014, 27 (12), 963-974.
\189. Ewender, J.; Welle, F. Determination of the activation energies of diffusion of organic molecules in poly(ethylene terephthalate). Journal of Applied Polymer Science 2018.
\190. Zhao, Y. H.; Abraham, M. H.; Zissimos, A. M. Fast Calculation of van der Waals Volume as a Sum of Atomic and Bond Contributions and Its Application to Drug Compounds. The Journal of Organic Chemistry 2003, 68 (19), 7368-7373.
\191. NIST NIST Chemistry WebBook. https://webbook.nist.gov/chemistry/ (accessed on March 31, 2019),
\192. Hinrichs, K.; Piringer, O. Evaluation of Migration Models to Be Used Under Directive 90/128/EEC; Final repot Contract SMT4-CT9867513. EUR 20604 EN. European Commission, Directorate General for Research 2002.
\193. Flynn, J. H. A collection of kinetic data for the diffusion of organic compounds in polyolefins. Polymer 1982, 23 (9), 1325-1344.
\194. Ewender, J.; Welle, F. Functional Barrier Performance of a Polyamide-6 Membrane Towards n-Alkanes and 1-Alcohols. Packaging Technology and Science 2016, 29 (6), 277-287.
\195. Boyne, J. A.; Williamson, A. G. Enthalpies of mixture of ethanol and water at 25.degree.C. Journal of Chemical & Engineering Data 1967, 12 (3), 318.
\196. Krüger, K.-M.; Sadowski, G. Fickian and Non-Fickian Sorption Kinetics of Toluene in Glassy Polystyrene. Macromolecules 2005, 38 (20), 8408-8417.
\197. Vitrac, O.; Hayert, M. Risk assessment of migration from packaging materials into foodstuffs. AIChE Journal 2005, 51 (4), 1080-1095.
\198. Vitrac, O.; Mougharbel, A.; Feigenbaum, A. Interfacial mass transport properties which control the migration of packaging constituents into foodstuffs. Journal of Food Engineering 2007, 79 (3), 1048-1064.
\199. Till, D.; Schwope, A. D.; Ehntholt, D. J.; Sidman, K. R.; Whelan, R. H.; Schwartz, P. S.; Reid, R. C.; Rainey, M. L. Indirect Food Additive Migration from Polymeric Food Packaging Materials. CRC Critical Reviews in Toxicology 1987, 18 (3), 215-243.
\200. Zhu, Y.; Guillemat, B.; Vitrac, O. Rational design of packaging: towards safer and eco-designed food packaging systems. accepted in Frontiers in Chemistry. Chemical Engineering. 2019.
\201. EFSA; WHO. Review of the Threshold of Toxicological Concern (TTC) approach and development of new TTC decision tree. EFSA Supporting Publications 2016, 13 (3), 1006E.
\202. Cramer, G. M.; Ford, R. A.; Hall, R. L. Estimation of toxic hazard—A decision tree approach. Food and Cosmetics Toxicology 1976, 16 (3), 255-276.
\203. CEN Materials modelling - Terminology, classification and metadata - CWA 17284 - https://www.cen.eu/news/workshops/Pages/WS-2017-012.aspx; EUROPEAN COMMITTEE FOR STANDARDIZATION: Brussels, Belgium, 2018; pp 1-18.